Voor een goed en betrouwbaar inzicht in de veiligheid van breedplaatvloeren is een probabilistische methode ontwikkeld, die rekening houdt met het zogenoemde track record (het presteren van de bestaande voorraad vloeren) van deze bouwwijze in de praktijk. In de probabilistische aanpak zijn alle onzekerheden gecombineerd om tot een uitspraak over de faalkans van de vloerconstructie te komen.
CEMENT 4 2024 ?49
Uitkomsten van experimenten aan
breedplaatvloeren geven weinig
vertrouwen in de in het verleden
toegepaste voegdetails [1].
Dat terwijl
er in Nederland veel gebouwen met dergelij-
ke vloeren bestaan. In de praktijk lijkt men
zich daar in bepaalde gevallen evenwel niet
uiterst ongemakkelijk bij te voelen; dit heeft
vermoedelijk te maken met de aanwezigheid
van de vele constructies die al geruime tijd
zonder problemen functioneren onder de
gebruikscondities tot dan toe. De wens is
een stap te zetten van deze informele niet
gekwantificeerde beschouwing naar een
formele gekwantificeerde beschouwing,
waarbij de uitkomst kan worden getoetst
aan een geaccepteerd criterium in de bouw -
regelgeving. Verder speelt de vraag hoe de meest
onveilige gebouwen snel kunnen worden
geïdentificeerd en indien nodig met voor- rang kunnen worden versterkt. En of daar-
bij een onderverdeling in vloertypologieën
mogelijk is. Om aan beide punten invulling te ge-
ven is een probabilistische aanpak van de
veiligheidsbeschouwing vereist, gebruikma -
kend van een track record.
Veiligheidsfilosofie voor bestaande
bouw bij gebruikmaking van track
record
In Eurocode 0 (NEN-EN 1990) worden ten
aanzien van constructieve veiligheid voor
nieuwbouw in hoofdstuk 2.1 in beginsel drie
eisen gesteld:
(a) Voldoende weerstand bieden tegen alle
belastingen en invloeden;
(b) Voldoende weerstand bieden tegen brand
gedurende een voorgeschreven tijdsperiode;
(c) Geen beschadiging oplopen bij buitenge-
wone belastingen en foutieve menselijke
Veiligheid bestaande
breedplaatvloeren op
basis van track record
Probabilistische achtergronden bij de veiligheid
van bestaande breedplaatvloeren
Voor een goed en betrouwbaar inzicht in de veiligheid van breedplaatvloeren is een
probabilistische methode ontwikkeld, die rekening houdt met het zogenoemde track record
(het presteren van de bestaande voorraad vloeren) van deze bouwwijze in de praktijk. In de probabilistische aanpak zijn alle onzekerheden gecombineerd om tot een uitspraak over de faalkans van de vloerconstructie te komen.
Nieuwe rekenregels bestaande breedplaatvloeren
50? CEMENT 4 2024
Informatie uit een 'mega-experiment' van
een groot aantal gebouwen, schaal 1 op 1, in
Nederland. Van één van deze gebouwen is
een vloer ingestort bij een bepaalde belas-
ting (dakvloer Eindhoven Airport) en bij
andere gebouwen hebben de bestaande
vloeren een bepaalde (zekere of onzekere)
belasting overleefd. We noemen dit een
'track record'. In dit mega-experiment zijn
alle genoemde zaken vallend onder de hier-
boven genoemde modelonzekerheid inbe-
grepen. Opgemerkt wordt dat het mega-
experiment plaatsvindt op het niveau van
'echte' complete constructies in plaats van
op het niveau van details, vloeren, liggers en
kolommen.
De volgens Annex D van NEN-EN 1990
vastgestelde gemiddelde waarde en stan -
daardafwijking van de modelonzekerheid
worden altijd bepaald voor een bepaald
toepassingsgebied of (sub)populatie. In dit
geheel is de keuze van een (sub)populatie
van groot belang. Het heeft bijvoorbeeld
geen zin de veiligheid van de breedplaat-
vloeren met een langsnaad ter plaatse van
het maximale veldmoment als veilig te kwa -
lificeren, door te wijzen op de grote groep
goed functionerende breedplaatvloeren
waar dit detail niet aanwezig is. Dergelijke
informatie is van belang en moet dus zorg -
vuldig worden meegenomen, in zoverre dat
dit mogelijk is op basis van de kennis van
verschillende typen detailleringen, uitvoe-
ringsvormen etc. Daar waar het mogelijk
is, zijn daarom in het onderhavige project
subpopulaties onderscheiden en beoor-
deeld (voor de definitie van de subpopula -
ties zie [3]).
Opzet faalkansberekening
In [2] is het bezwijken van de voeg tussen
twee breedplaten beschreven via vier faal -
mechanismen:
1 Bezwijken ongewapend aansluitvlak op
aanhechting;
2 Bezwijken gewapend aansluitvlak op
afschuiving;
3 Bezwijken gewapend aansluitvlak door
uittrekken van de tralieligger;
4 Bezwijken na vloeien van de koppelwape-
ning.
PROF.DR.IR. RAPHAEL
STEENBERGEN
TNO / UGent
IR. REIN DE VRIES TNO / TU Delft
PROF.IR. TON
VROUWENVELDER
TNO
auteurs
handelingen die niet in verhouding staat tot
de oorzaak.
Delen van NEN-EN 1990 zijn door het Bouw -
besluit 2012 aangewezen, waarmee de be-
treffende eisen publiekrechtelijk zijn. Voor
(c) kiest het Bouwbesluit 2012 deels een
strengere eis dan NEN-EN 1990 (het gaat
niet om disproportioneel 'bezwijken', maar
om het niet mogen bezwijken van niet direct
aangrenzende constructieve onderdelen).
Minder streng is dat het Bouwbesluit 2012
alleen kijkt naar gekende buitengewone
belastingen. Voor bestaande bouw zijn de
eisen onder (c) helemaal vervallen en zijn de
eisen gerelateerd aan (a) en (b) verlicht ten
opzichte van nieuwbouw in NEN 8700.
In de gebruikte probabilistische beoorde-
lingsmethode wordt de in de praktijk aan -
wezige bestaande weerstand van de breed -
platen zo goed mogelijk gekwantificeerd, en
meegenomen via een variabele die wordt
aangeduid als de modelonzekerheid. In de
terminologie van de betrouwbaarheidstheo-
rie worden hiermee aspecten bedoeld die
wel invloed hebben op de sterkte, maar niet
of niet volledig in het model zijn meegeno-
men. Immers, in elk rekenmodel worden
vereenvoudigingen aangebracht die bij elke
individuele toepassing tot een grotere of
kleinere, positieve dan wel negatieve afwij-
king leiden van de theoretische waarde.
In de basis wordt voor de uitwerking alle be-
schikbare informatie over de betrouwbaar-
heid van bestaande breedplaatvloeren ge-
bruikgemaakt van de procedures in NEN-EN
1990 Annexen C en D. Deze procedures vor-
men ook de achtergrond voor de veiligheids-
factoren in de Eurocodes en de kalibratie
van de partiële factoren in de normen zoals
aangegeven in de nationale bijlagen van in
het Bouwbesluit aangewezen normen.
In de onderhavige studie worden twee typen
experimenten meegenomen:
Informatie vanuit de beschikbare labora -
toriumproeven. In deze experimenten
wordt een aantal malen falen en een aantal
malen overleven waargenomen bij een be-
paalde belasting.
Belastin g o p d e ta il
1
Be zw ijk e n
o ng ew ap e nd d e el
a an sluit vla k doo r
b ezw ij k e n v a n
hech ting
2
Be zw ijk en
g e w ap en d d eel
a a nslu it v la k doo r
b e zw ij k e n o p
a fs ch u iv in g
3
Be zw ijk e n
g ew ape nd deel
a an sluit vla k doo r
uittre kke n
tralie ligger
4
Be zw ijk en
k o p pe lw apeni ng
do or vlo ei
CEMENT 4 2024 ?51
In het systeemgedrag staan faalmechanis-
men 1 t/m 3 parallel geschakeld en vervol -
gens gezamenlijk in serie met mechanisme 4,
het vloeien van de koppelwapening (fig. 1). De
constructie bezwijkt dus als mechanisme 4
zich voordoet of als een van de eerste drie
mechanismen optreedt. De overige faalme-
chanismen van de breedplaatvloer zijn in de
praktijk afgedekt door een correct ontwerp
conform de normen en zijn niet verder be-
schouwd.
In een probabilistische berekening wordt de
verwerking van de faalmechanismen meege
-
nomen met behulp van de grenstoestands -
functies (g(..)). Deze functies van stochasten
zijn gedefinieerd als het verschil tussen de
sterkte en het belasting(effect). Een negatief
verschil komt overeen met bezwijken, een
positief verschil met overleven. Er wordt
daarbij niet alleen rekening gehouden met de
maximale capaciteit van het mechanisme,
maar ook met de (mogelijk beperkt aanwezige)
ductiliteit in de mechanismen 1, 2 en 3.
De kans P op de gebeurtenis falen F van een
te beoordelen vloerconstructie wordt in een
probabilistische berekening gegeven door: P(F) = P(g < 0)
(1)
Hierbij is g(..) de grenstoestandsfunctie voor
de combinatie van vier geïntroduceerde
mechanismen. De grenstoestandsfuncties
worden voor ieder faalmechanisme apart
berekend, resulterend in waarden g
R1 t/m g R4.
Om de uiteindelijke g-waarde te bepalen
moeten deze vier functies dus gecombineerd
worden. De mechanismen 1, 2 en 3 zijn zoals
eerder gezegd onderling parallel geschakeld:
bezwijken treedt op als een van deze drie
functies negatief wordt. Dat is wiskundig
het geval als de grootste waarde ofwel het
maximum van [g
R1, gR2, gR3] negatief wordt.
Bezwijken treedt echter ook op als g
R4 nega -
tief wordt. Wiskundig bepalend wordt daar-
mee de kleinste waarde van het minimum
van g
R4 en het maximum van [g R1, gR2, gR3].
De uiteindelijke g-waarde waarmee wordt
bepaald of falen optreedt (g < 0), volgt uit
daarmee uit:
g = min (max[g
R1, gR2, gR3], g R4) (2)
De bewerking 'max' is in deze uitdrukking
dus van toepassing op de functies van de
mechanismen 1, 2 en 3; de bewerking
1 Schematische weergave combinatie van faalmechanismen van de voeg. Mechanismen 1-3 staan parallel geschakeld,
mechanismen 1-3 samen staan in serie met mechanisme 4. Voor bezwijken is het dus voldoende als mechanisme 4 optreedt
of een van de mechanismen 1-3
1
Nieuwe rekenregels bestaande breedplaatvloeren
52? CEMENT 4 2024
'min' is van toepassing op de functie van
mechanisme 4 en het maximum van 1, 2 en 3.
De afzonderlijke grenstoestandsfuncties
worden geschreven als g = R - (G + Q), met R
de sterkte, G de eigengewichtsbelasting en
Q de veranderlijke belasting. De sterkte R in
het werkelijke gebouw wordt hier geschreven
als een modelonzekerheid ?
R maal de sterkte
volgend uit de laboratoriumexperimenten
R
exp. Het track record van de constructie
zelf en van vergelijkbare constructies wordt
tot uitdrukking gebracht door P(F) in (1) te
vervangen door:
P(F | D) = P(g < 0 | D) (3)
Hierbij is de sterkte op basis van laboratori -
umtesten meegenomen in de grenstoestands-
functie g en stelt D de verzameling van alle
relevante data (waarnemingen in het 'mega-
experiment') voor. De verticale streep in (3)
moet worden gelezen als 'gegeven', het gaat
dus om de kans op falen gegeven de data
beschikbaar in het track record.
De verzameling van relevante waarnemingen
kan als volgt worden samengevat:
Het goed functioneren van de beschouwde
vloer over een aantal jaren t;
Het goed functioneren van een groep van
vergelijkbare vloeren over een aantal jaren
en/of het met succes doorstaan van een
proefbelasting;
Het instorten van de dakvloer in de par-
keergarage op Eindhoven Airport en het niet
instorten van de overige vloeren op Eindho-
ven Airport.
Genoteerd in termen van falen (F) of overle-
ven (S, survival) kan dus de beschikbare
verzameling waarnemingen D worden ge-
schreven als:
D = [S, S
1, S2, ?, S n, FE,1, SE,1, ?, S E,m] (4)
Hierin staat S voor het overleven (de survi -
val) vanaf de bouw tot op heden van de
beschouwde vloer zelf. S
i staat voor het over-
leven van een vergelijkbare andere vloer i,
eveneens vanaf de bouw tot heden al dan
niet inclusief het doorstaan van een proef -belasting. F
E,1 is het falen (instorten) van de
vloer van de parkeergarage in aanbouw bij
de luchthaven Eindhoven. S
E,j staat voor het
tot op heden overleven van de niet bezweken
vloeren van de parkeergarage in aanbouw
bij de luchthaven Eindhoven. Al deze gebeurtenissen zijn vervol -
gens weer uit te drukken in termen van
grenstoestandsfuncties (let hierbij op het
verschil in >- en 0} (5a)
F
E,1 = {g E (X) < 0)} (5b)
S
E,j = {g E(X) > 0)} (5c)
De g-functies van de stochasten X worden
voor alle gebouwen uitgewerkt waarbij ver
-
schillende subpopulaties worden onderschei -
den. De g E-functie betreft de grenstoestands -
functie voor de vloeren in Eindhoven Airport.
Lang niet alle vloeren zijn gelijk qua
afmetingen, legpatroon en voegdetails. In
het project zijn daarom 12 subpopulaties
onderscheiden (zie [2]). De berekening van de kans is gepro-
grammeerd via Monte Carlo-simulatie.
Betrouwbaarheid
Om de betrouwbaarheid van een bestaande
breedplaatvloer te beoordelen, wordt met
behulp van het model een analyse uitgevoerd
waarbij het presteren van andere vloeren ook
in beschouwing wordt genomen. Er wordt ge -
rekend met een aantal van n gebouwen van
een bepaalde subpopulatie (uit het 'track
record'), met per gebouw (gemiddeld) 30
niet gefaalde vloervelden (uitgezonderd bij
dakvloeren, waar gerekend wordt met 5 niet
gefaalde vloervelden per gebouw), aangevuld
met van het gebouw Eindhoven Airport:
de gefaalde dakvloer;
niet gefaalde tussenvloeren;
een niet gefaalde naastliggende dakvloer
alleen belast door eigen gewicht.
Voor 'niet falen' van de vloeren in de n ge -
bouwen wordt uitgegaan van de eerste
10 jaar van de levensduur. Deze 10 jaar is
een voorzichtig (conservatief ) gekozen
waarde voor de leeftijd van de n gebouwen,
gegeven het bouwjaar van veel Nederlandse
gebouwen met breedplaatvloeren.
Afstand verwachtingswaarde sterkte en verwachtingswaarde belasting
kansdichtheid
Bewezen sterkte
Sterkte, belasting
Groen: zonder bewezen sterkte
Blauw: met bewezen sterkte
CEMENT 4 2024 ?53
2 3
2 Principe van bewezen sterkte
3 Bewezen sterkte en updaten
Pf = P(falen beschouwde vloer in 0-15 jaar |
1 x falen Eindhoven dakvloer zonder Q en met
T ?
8 x niet falen Eindhoven verdiepingsvloer
zonder Q ?
n x niet falen gebouwen met 30 vloeren in
0-10 jaar)
Gegeven de faalkans, is de betrouwbaar-
heidsindex te vinden via de tabel voor de
normale verdeling. Hoe meer gebouwen die
goed presteren, hoe hoger de betrouwbaar-
heid. In bovenstaande faalkansberekening
wordt gewerkt met een referentieperiode
van 15 jaar. Dit is gedaan omdat voor het
af eurniveau in NEN 8700 deze referentie-
periode is voorgeschreven. We kijken dus
naar een faalkans in een periode van 15 jaar
volgend op de beoordeling. Voor hetzelfde type vloer, maar kij-
kend naar de periode 5-20 jaar (dus onder
voorwaarde dat de beschouwde vloer niet
heeft gefaald in de eerste 5 jaar), wordt de
kans bepaald als:
P
f = P(falen beschouwde vloer in 5-20 jaar |
1 x falen Eindhoven dakvloer zonder Q en
met T ?
8 x niet falen Eindhoven verdiepingsvloer
zonder Q ?
n x niet falen gebouwen met 30 vloeren in
0-10 jaar) ?
1 x niet falen beschouwde vloer in 0-5 jaar)
Op dezelfde wijze kan dan worden gekeken
naar een periode 10-25 jaar (dus onder voor-
waarde dat de beschouwde vloer niet heeft
gefaald in de eerste 10 jaar), en ook verder in
de tijd.
BEWEZEN STERKTE
Het algemene principe van bewezen sterkte bij bestaande constructies is dat op
basis van een zonder problemen (zoals een instorting) overleefde belastingobser-
vatie de faalkans wordt bijgesteld. Deze faalkans (voor een jaar of anderszins
zinvolle periode) wordt namelijk in de gebruikelijke (semi-)probabilistische
methoden bepaald zonder deze bijstelling, hetgeen conservatief is. De overleefde
belasting toont aan dat bepaalde waardes van de modelonzekerheid en/of de
sterkteparameters waarschijnlijk worden onderschat of de belasting overschat.
In figuur 2 is dit weergegeven voor de verdeling van de belasting (eigengewichts-
belasting en vloerbelasting) en een verdeling van de sterkte (opgebouwd uit de
op basis van laboratoriumexperimenten bepaalde sterkte en een modelonzeker-
heid). Met de observatie op een bepaald ogenblik van een bepaalde belasting
(oranje stippellijn) kan een sterkte lager dan deze observatie voor die constructie
kennelijk niet voorkomen. De kansdichtheid van de sterkte die niet kan voorko-
men (het lichtblauw gekleurde deel links van de stippellijn) wordt (overeenkom-
stig de regels van de kansrekening) herverdeeld over de rest van de sterkte (het
lichtblauw gekleurde deel rechts van de stippellijn). Het effect hiervan is dat de
verwachte sterkte enigszins groter is dan voor de observatie, wat de faalkans
vervolgens doet afnemen. Er is echter voornamelijk een effect te zien van reduce-
ring van de spreiding in de linker staart van de sterkte. Dit kan afhankelijk van de
onzekerheid in de linker staart een grote invloed hebben op de faalkans. In het
onderhavige geval van de beoordeling van breedplaatvloeren is vanwege de
grote spreiding in de experimenteel bepaalde sterkte en in de modelonzekerheid
aan de sterktekant, het effect van bewezen sterkte inderdaad significant.
De verschuiving zoals getekend in lichtblauw in figuur 2 geldt alleen voor een
belasting met bekende grootte gelijk aan de stippellijn. Bij een belasting met
onbekende grootte (rode lijn) vlakt de update met bewezen sterkte enigszins uit.
We krijgen dan situatie zoals geschetst in figuur 3.
De kans op falen van een bepaalde te analy -
seren vloer in de eerste 15 jaar van de levens -
duur wordt als volgt berekend (het |-teken
in het onderstaande moet weer worden gele-
zen als 'gegeven' of 'onder de conditie dat' en
het ?-teken als 'en', T staat voor belasting
door temperatuur):
Nieuwe rekenregels bestaande breedplaatvloeren
0
1
2
3
4
5
6
7
0,
11 101001 000
Betrouw .-index per 15 jaar (
)
Aantal gebouw en 10 jaar overleefd ( )
Geval 1
Ge val 2
Ge val 3
Ge val 4
Ge val 5
Ge val 6 Verdiepingsvloer
Periode 0-15 jaar
0
0
1
2
3
4
5
6
7
0,
11 1010 01 000
Betrouw.-index per 15 jaar (
)
Aantal gebouw en 10 jaar overleefd ( )
Geval 7
Ge val 8
Ge val 9
Ge val 10
Ge val 11
Ge val 12 Verdiepingsvloer
Periode 0-15 jaar
0
0
1
2
3
4
5
6
7
0,
11 101001 000
Betrouw .-index per 15 jaar (
)
Aantal gebouw en 10 jaar overleefd ( )
Geval 1
Ge val 2
Ge val 3
Ge val 4
Ge val 5
Ge val 6 Verdiepingsvloer
Periode 5-20 jaar
0
0
1
2
3
4
5
6
7
0,
11 1010 01 000
Betrouw.-index per 15 jaar (
)
Aantal gebouw en 10 jaar overleefd ( )
Geval 7
Ge val 8
Ge val 9
Ge val 10
Ge val 11
Ge val 12 Verdiepingsvloer
Periode 5-20 jaar
0
54? CEMENT 4 2024
Er wordt onderscheid gemaakt tussen nor-
male (tussen)vloeren en dakvloeren. Bij niet
geïsoleerde dakvloeren wordt extra gekeken
naar effecten van opgelegde vervormingen
door krimp of temperatuur.
Berekeningsuitkomsten
In [2] zijn voor alle 12 subpopulaties en
leeftijden probabilistische berekeningen
uitgevoerd inclusief een groot aantal varia -
tiestudies. Voor de exacte definitie van de
subpopulaties wordt verwezen naar [2]. Ter
illustratie worden hieronder enkele bereke-
ningen getoond. In figuren 4 en 5 is het betrouwbaar-
heidsniveau van een te beoordelen breed -
plaatvloer weergegeven (uitgedrukt in een
?-waarde voor een referentieperiode van
15 jaar volgend op de beoordeling conform
NEN 8700 voor het af eurniveau). Voor elk van de subpopulaties geldt een afzonderlijke
lijn. In figuur 4 is de betrouwbaarheid weer-
gegeven voor een constructie beschouwd op
t = 0; met andere woorden zonder bewezen
sterkte van diezelfde constructie in de tijd.
In figuur 5 is de betrouwbaarheid beschouwd
op t = 5 jaar, met andere woorden een be-
staande constructie van minimaal 5 jaar
oud. Op de horizontale as is de informatie-
basis vanuit het track record gegeven. Dit
geeft aan wat het effect is op de betrouw -
baarheid als gevolg van het aantal succesvol
presterende gebouwen met een vergelijkba -
re vloeropbouw. Of anders gezegd het aantal
benodigde succesvolle gebouwen om een
bepaalde betrouwbaarheid aan te tonen. Er
is op de horizontale as van de figuren niet
direct uitgegaan van een daadwerkelijk be-
schikbaar track record, maar er wordt van
uitgegaan dat een track record met n gebou -
5
4
4 Betrouwbaarheidsindex in periode 0-15 jaar versus het aantal vergelijkbare gebouwen dat 10 jaar heeft gefunctioneerd
5 Betrouwbaarheidsindex in periode 5-20 jaar versus het aantal vergelijkbare gebouwen dat 10 jaar heeft gefunctioneerd.
De horizontale stippellijn geeft het afkeurniveau CC2 aan conform NEN 8700
CEMENT 4 2024 ?55
wen beschikbaar zou zijn. Uit de grafiek kan
dus afgelezen worden hoeveel gebouwen er
in een track record moeten zitten, om te
kunnen zeggen dat de
?-waarde voldoende
groot is. Voor de gebouwen uit het track re-
cord (niet zijnde het gebouw dat beoordeeld
wordt) wordt uitgegaan van een voorzichtig
gekozen gemiddelde van 10 jaar succesvol
presteren.
Doordat informatie beschikbaar is over het
succesvol presteren van de eigen of andere
vloerconstructies, wordt het minder waar-
schijnlijk dat de constructie een lage faal -
kans heeft; in de figuren 4 en 5 vertoont het
verloop van de betrouwbaarheid een stijgen -
de lijn met toenemende n. Met behulp van
de theorie worden de schattingen van ge-
middelde en standaardafwijking bijgesteld
(geüpdate); het gemiddelde wordt groter, de
spreiding kleiner. Bij een probabilistische
berekening levert dit een kleinere faalkans
op. Bij een semi-probabilistische beschou -
wing leidt dit tot een hogere rekenwaarde
van de weerstand en daarmee een afname
van de Unity Check. Ook is te zien dat de te
beoordelen vloerconstructie een eigen be-
wezen sterkte in de tijd heeft; de waarden
voor de betrouwbaarheid liggen hoger in
figuur 5 dan in figuur 4. Ten slotte zijn de
12 subpopulaties zichtbaar met een duidelijk
verschillend verloop van de betrouwbaar-
heid.
Conclusie
TNO heeft een betrouwbaarheidsanalyse uit-
gevoerd voor de beoordeling van bestaande
Nederlandse breedplaatvloerconstructies
waarbij sprake is van primaire krachtsover-
dracht (buigende momenten in het midden
van een overspanning) over het constructie-
detail ter plaatse van de langsnaden of
langsvoegen tussen de breedplaten. Geko-
zen is voor het ontwikkelen van een proba -
bilistische beoordelingsmethode. Met deze
methode is het mogelijk om alle typen in -
formatie over de constructieve sterkte en
alle onzekerheden op een verantwoorde
wijze mee te nemen en de vloeren direct te
toetsen aan de in de vigerende regelgeving
vereiste betrouwbaarheid. Zowel informatie
uit laboratoriumproeven over het gedrag van de naad en informatie uit het track
record van bestaande vloerconstructies is
verwerkt. Het track record bevat het falen
van de dakvloer bij de parkeergarage van
Eindhoven Airport, evenals het niet falen
(overleven) van vloeren van gebouwen met
breedplaatvloeren onder opgetreden ge-
bruiksbelastingen en proefbelastingen.
Conclusie: In aanleg kunnen grote vraag-
tekens worden geplaatst bij de constructieve
veiligheid van breedplaatvloeren gebouwd
tot 2017 waarbij primaire krachtsafdracht
plaats moet vinden bij de langsvoeg. Dit is
het gevolg van de rekenkundig gezien on-
voldoende detaillering ter plaatse van de
langsvoeg. Door combinatie van de reken -
modellen, de uitkomsten van laboratorium -
proeven en de bewezen sterkte analyse kan
echter worden geconcludeerd dat voor be-
paalde gebouwtypologieën de vloeren toch
voldoende betrouwbaar zijn. Voor de conclusies op niveau van de
verschillende subpopulaties wordt verwezen
naar [2]]. Bijzondere aandacht is daarin ge-
vraagd voor direct door zonlicht bestraalde
dakvloeren en grote overspanningen (10-15m);
deze voldoen na analyse niet aan de betrouw -
baarheidseis voor CC2 uit NEN 8700 en de
betrouwbaarheid is zeer laag.
LITERATUUR
1?Wijte, S., & Dieteren, G., Rekenregels
beoordeling bestaande
breedplaatvloeren. Cement 2019/4.
2?Steenbergen, R., Dieteren, G., Vries, R.
de, Borsje, H., Vrouwenvelder, T., & Wijte,
S. TNO-2022-R10122 Probabilistische
kwantificering van de veiligheid van
bestaande breedplaatvloeren. Delft:
TNO, 2022.
3?Wijte, S., & Dieteren, G.,
Vereenvoudigde beoordelingsprocedure
breedplaatvloeren. Cement 2024/4.
Nieuwe rekenregels bestaande breedplaatvloeren
Uitkomsten van experimenten aan breedplaatvloeren geven weinig vertrouwen in de in het verleden toegepaste voegdetails [1]. Dat terwijl er in Nederland veel gebouwen met dergelijke vloeren bestaan. In de praktijk lijkt men zich daar in bepaalde gevallen evenwel niet uiterst ongemakkelijk bij te voelen; dit heeft vermoedelijk te maken met de aanwezigheid van de vele constructies die al geruime tijd zonder problemen functioneren onder de gebruikscondities tot dan toe. De wens is een stap te zetten van deze informele niet gekwantificeerde beschouwing naar een formele gekwantificeerde beschouwing, waarbij de uitkomst kan worden getoetst aan een geaccepteerd criterium in de bouwregelgeving.
Verder speelt de vraag hoe de meest onveilige gebouwen snel kunnen worden geïdentificeerd en indien nodig met voorrang kunnen worden versterkt. En of daarbij een onderverdeling in vloertypologieën mogelijk is.
Om aan beide punten invulling te geven is een probabilistische aanpak van de veiligheidsbeschouwing vereist, gebruikmakend van een track record.
Veiligheidsfilosofie voor bestaande bouw bij gebruikmaking van track record
In Eurocode 0 (NEN-EN 1990) worden ten aanzien van constructieve veiligheid voor nieuwbouw in hoofdstuk 2.1 in beginsel drie eisen gesteld:
- Voldoende weerstand bieden tegen alle belastingen en invloeden;
- Voldoende weerstand bieden tegen brand gedurende een voorgeschreven tijdsperiode;
- Geen beschadiging oplopen bij buitengewone belastingen en foutieve menselijke handelingen die niet in verhouding staat tot de oorzaak.
Delen van NEN-EN 1990 zijn door het Bouwbesluit 2012 aangewezen, waarmee de betreffende eisen publiekrechtelijk zijn. Voor (c) kiest het Bouwbesluit 2012 deels een strengere eis dan NEN-EN 1990 (het gaat niet om disproportioneel ‘bezwijken’, maar om het niet mogen bezwijken van niet direct aangrenzende constructieve onderdelen). Minder streng is dat het Bouwbesluit 2012 alleen kijkt naar gekende buitengewone belastingen. Voor bestaande bouw zijn de eisen onder (c) helemaal vervallen en zijn de eisen gerelateerd aan (a) en (b) verlicht ten opzichte van nieuwbouw in NEN 8700.
In de gebruikte probabilistische beoordelingsmethode wordt de in de praktijk aanwezige bestaande weerstand van de breedplaten zo goed mogelijk gekwantificeerd, en meegenomen via een variabele die wordt aangeduid als de modelonzekerheid. In de terminologie van de betrouwbaarheidstheorie worden hiermee aspecten bedoeld die wel invloed hebben op de sterkte, maar niet of niet volledig in het model zijn meegenomen. Immers, in elk rekenmodel worden vereenvoudigingen aangebracht die bij elke individuele toepassing tot een grotere of kleinere, positieve dan wel negatieve afwijking leiden van de theoretische waarde.
In de basis wordt voor de uitwerking alle beschikbare informatie over de betrouwbaarheid van bestaande breedplaatvloeren gebruikgemaakt van de procedures in NEN-EN 1990 Annexen C en D. Deze procedures vormen ook de achtergrond voor de veiligheidsfactoren in de Eurocodes en de kalibratie van de partiële factoren in de normen zoals aangegeven in de nationale bijlagen van in het Bouwbesluit aangewezen normen.
In de onderhavige studie worden twee typen experimenten meegenomen:
- Informatie vanuit de beschikbare laboratoriumproeven. In deze experimenten wordt een aantal malen falen en een aantal malen overleven waargenomen bij een bepaalde belasting.
- Informatie uit een ‘mega-experiment’ van een groot aantal gebouwen, schaal 1 op 1, in Nederland. Van één van deze gebouwen is een vloer ingestort bij een bepaalde belasting (dakvloer Eindhoven Airport) en bij andere gebouwen hebben de bestaande vloeren een bepaalde (zekere of onzekere) belasting overleefd. We noemen dit een ‘track record’. In dit mega-experiment zijn alle genoemde zaken vallend onder de hierboven genoemde modelonzekerheid inbegrepen. Opgemerkt wordt dat het mega-experiment plaatsvindt op het niveau van ‘echte’ complete constructies in plaats van op het niveau van details, vloeren, liggers en kolommen.
De volgens Annex D van NEN-EN 1990 vastgestelde gemiddelde waarde en standaardafwijking van de modelonzekerheid worden altijd bepaald voor een bepaald toepassingsgebied of (sub)populatie. In dit geheel is de keuze van een (sub)populatie van groot belang. Het heeft bijvoorbeeld geen zin de veiligheid van de breedplaatvloeren met een langsnaad ter plaatse van het maximale veldmoment als veilig te kwalificeren, door te wijzen op de grote groep goed functionerende breedplaatvloeren waar dit detail niet aanwezig is. Dergelijke informatie is van belang en moet dus zorgvuldig worden meegenomen, in zoverre dat dit mogelijk is op basis van de kennis van verschillende typen detailleringen, uitvoeringsvormen etc. Daar waar het mogelijk is, zijn daarom in het onderhavige project subpopulaties onderscheiden en beoordeeld (voor de definitie van de subpopulaties zie [3]).
Opzet faalkansberekening
In [2] is het bezwijken van de voeg tussen twee breedplaten beschreven via vier faalmechanismen:
- Bezwijken ongewapend aansluitvlak op aanhechting;
- Bezwijken gewapend aansluitvlak op afschuiving;
- Bezwijken gewapend aansluitvlak door uittrekken van de tralieligger;
- Bezwijken na vloeien van de koppelwapening.
In het systeemgedrag staan faalmechanismen 1 t/m 3 parallel geschakeld en vervolgens gezamenlijk in serie met mechanisme 4, het vloeien van de koppelwapening (fig. 1). De constructie bezwijkt dus als mechanisme 4 zich voordoet of als een van de eerste drie mechanismen optreedt. De overige faalmechanismen van de breedplaatvloer zijn in de praktijk afgedekt door een correct ontwerp conform de normen en zijn niet verder beschouwd.
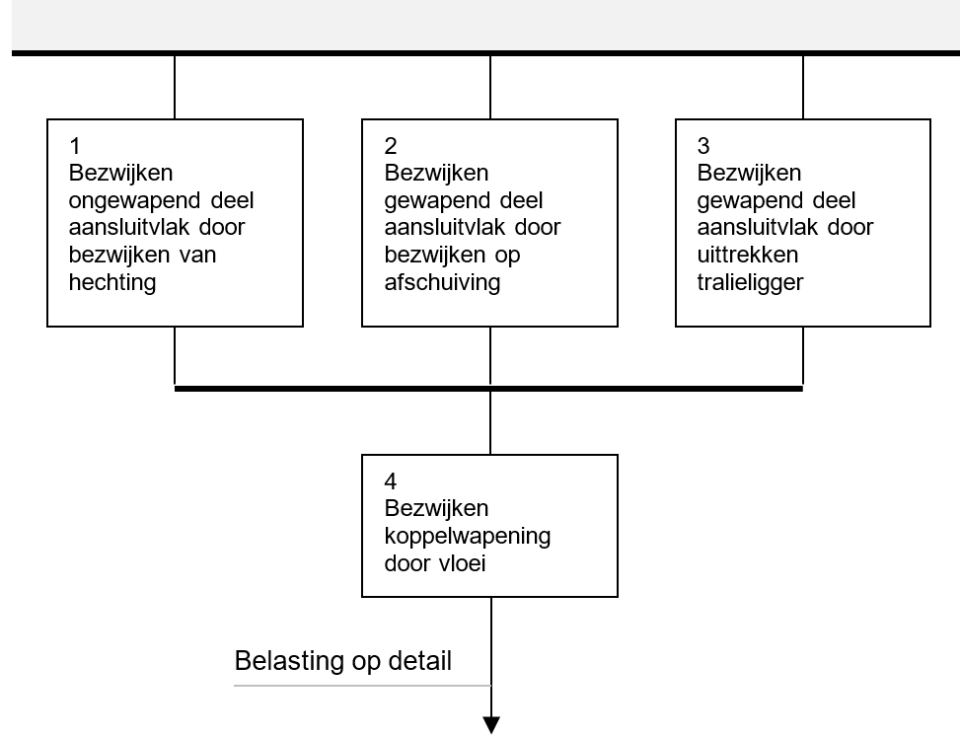
Figuur 1. Schematische weergave combinatie van faalmechanismen van de voeg. Mechanismen 1-3 staan parallel geschakeld, mechanismen 1-3 samen staan in serie met mechanisme 4. Voor bezwijken is het dus voldoende als mechanisme 4 optreedt of een van de mechanismen 1-3
In een probabilistische berekening wordt de verwerking van de faalmechanismen meegenomen met behulp van de grenstoestandsfuncties (g(..)). Deze functies van stochasten zijn gedefinieerd als het verschil tussen de sterkte en het belasting(effect). Een negatief verschil komt overeen met bezwijken, een positief verschil met overleven. Er wordt daarbij niet alleen rekening gehouden met de maximale capaciteit van het mechanisme, maar ook met de (mogelijk beperkt aanwezige) ductiliteit in de mechanismen 1, 2 en 3.
De kans P op de gebeurtenis falen F van een te beoordelen vloerconstructie wordt in een probabilistische berekening gegeven door:
P(F) = P(g < 0) (1)
Hierbij is g(..) de grenstoestandsfunctie voor de combinatie van vier geïntroduceerde mechanismen. De grenstoestandsfuncties worden voor ieder faalmechanisme apart berekend, resulterend in waarden gR1 t/m gR4. Om de uiteindelijke g-waarde te bepalen moeten deze vier functies dus gecombineerd worden. De mechanismen 1, 2 en 3 zijn zoals eerder gezegd onderling parallel geschakeld: bezwijken treedt op als een van deze drie functies negatief wordt. Dat is wiskundig het geval als de grootste waarde ofwel het maximum van [gR1, gR2, gR3] negatief wordt. Bezwijken treedt echter ook op als gR4 negatief wordt. Wiskundig bepalend wordt daarmee de kleinste waarde van het minimum van gR4 en het maximum van [gR1, gR2, gR3]. De uiteindelijke g-waarde waarmee wordt bepaald of falen optreedt (g < 0), volgt uit daarmee uit:
g = min (max[gR1, gR2, gR3], gR4) (2)
De bewerking ‘max’ is in deze uitdrukking dus van toepassing op de functies van de mechanismen 1, 2 en 3; de bewerking ‘min’ is van toepassing op de functie van mechanisme 4 en het maximum van 1, 2 en 3.
De afzonderlijke grenstoestandsfuncties worden geschreven als g = R - (G + Q), met R de sterkte, G de eigengewichtsbelasting en Q de veranderlijke belasting. De sterkte R in het werkelijke gebouw wordt hier geschreven als een modelonzekerheid θR maal de sterkte volgend uit de laboratoriumexperimenten Rexp.
Het track record van de constructie zelf en van vergelijkbare constructies wordt tot uitdrukking gebracht door P(F) in (1) te vervangen door:
P(F | D) = P(g < 0 | D) (3)
Hierbij is de sterkte op basis van laboratoriumtesten meegenomen in de grenstoestandsfunctie g en stelt D de verzameling van alle relevante data (waarnemingen in het ‘mega-experiment’) voor. De verticale streep in (3) moet worden gelezen als ‘gegeven’, het gaat dus om de kans op falen gegeven de data beschikbaar in het track record.
De verzameling van relevante waarnemingen kan als volgt worden samengevat:
- Het goed functioneren van de beschouwde vloer over een aantal jaren t;
- Het goed functioneren van een groep van vergelijkbare vloeren over een aantal jaren en/of het met succes doorstaan van een proefbelasting;
- Het instorten van de dakvloer in de parkeergarage op Eindhoven Airport en het niet instorten van de overige vloeren op Eindhoven Airport.
Genoteerd in termen van falen (F) of overleven (S, survival) kan dus de beschikbare verzameling waarnemingen D worden geschreven als:
D = [S, S1, S2, …, Sn, FE,1, SE,1, …, SE,m] (4)
Hierin staat S voor het overleven (de survival) vanaf de bouw tot op heden van de beschouwde vloer zelf. Si staat voor het overleven van een vergelijkbare andere vloer i, eveneens vanaf de bouw tot heden al dan niet inclusief het doorstaan van een proefbelasting. FE,1 is het falen (instorten) van de vloer van de parkeergarage in aanbouw bij de luchthaven Eindhoven. SE,j staat voor het tot op heden overleven van de niet bezweken vloeren van de parkeergarage in aanbouw bij de luchthaven Eindhoven.
Al deze gebeurtenissen zijn vervolgens weer uit te drukken in termen van grenstoestandsfuncties (let hierbij op het verschil in >- en <-tekens):
Si = {gi (X) > 0} (5a)
FE,1 = {gE (X) < 0)} (5b)
SE,j = {gE(X) > 0)} (5c)
De g-functies van de stochasten X worden voor alle gebouwen uitgewerkt waarbij verschillende subpopulaties worden onderscheiden. De gE-functie betreft de grenstoestandsfunctie voor de vloeren in Eindhoven Airport.
Lang niet alle vloeren zijn gelijk qua afmetingen, legpatroon en voegdetails. In het project zijn daarom 12 subpopulaties onderscheiden (zie [2]).
De berekening van de kans is geprogrammeerd via Monte Carlo-simulatie.
Bewezen sterkte
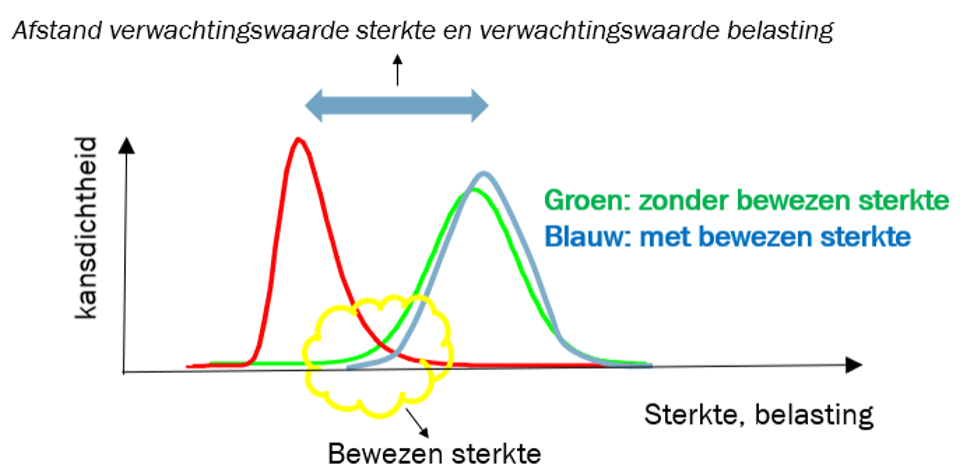
Het algemene principe van bewezen sterkte bij bestaande constructies is dat op basis van een zonder problemen (zoals een instorting) overleefde belastingobservatie de faalkans wordt bijgesteld. Deze faalkans (voor een jaar of anderszins zinvolle periode) wordt namelijk in de gebruikelijke (semi-)probabilistische methoden bepaald zonder deze bijstelling, hetgeen conservatief is. De overleefde belasting toont aan dat bepaalde waardes van de modelonzekerheid en/of de sterkteparameters waarschijnlijk worden onderschat of de belasting overschat. In figuur 2 is dit weergegeven voor de verdeling van de belasting (eigengewichtsbelasting en vloerbelasting) en een verdeling van de sterkte (opgebouwd uit de op basis van laboratoriumexperimenten bepaalde sterkte en een modelonzekerheid). Met de observatie op een bepaald ogenblik van een bepaalde belasting (oranje stippellijn) kan een sterkte lager dan deze observatie voor die constructie kennelijk niet voorkomen. De kansdichtheid van de sterkte die niet kan voorkomen (het lichtblauw gekleurde deel links van de stippellijn) wordt (overeenkomstig de regels van de kansrekening) herverdeeld over de rest van de sterkte (het lichtblauw gekleurde deel rechts van de stippellijn). Het effect hiervan is dat de verwachte sterkte enigszins groter is dan voor de observatie, wat de faalkans vervolgens doet afnemen. Er is echter voornamelijk een effect te zien van reducering van de spreiding in de linker staart van de sterkte. Dit kan afhankelijk van de onzekerheid in de linker staart een grote invloed hebben op de faalkans. In het onderhavige geval van de beoordeling van breedplaatvloeren is vanwege de grote spreiding in de experimenteel bepaalde sterkte en in de modelonzekerheid aan de sterktekant, het effect van bewezen sterkte inderdaad significant.
De verschuiving zoals getekend in lichtblauw in figuur 2 geldt alleen voor een belasting met bekende grootte gelijk aan de stippellijn. Bij een belasting met onbekende grootte (rode lijn) vlakt de update met bewezen sterkte enigszins uit. We krijgen dan situatie zoals geschetst in figuur 3.

Figuur 2. Principe van bewezen sterkte
Figuur 3. Bewezen sterkte en updaten
Betrouwbaarheid
Om de betrouwbaarheid van een bestaande breedplaatvloer te beoordelen, wordt met behulp van het model een analyse uitgevoerd waarbij het presteren van andere vloeren ook in beschouwing wordt genomen. Er wordt gerekend met een aantal van n gebouwen van een bepaalde subpopulatie (uit het ’track record’), met per gebouw (gemiddeld) 30 niet gefaalde vloervelden (uitgezonderd bij dakvloeren, waar gerekend wordt met 5 niet gefaalde vloervelden per gebouw), aangevuld met van het gebouw Eindhoven Airport:
- de gefaalde dakvloer;
- niet gefaalde tussenvloeren;
- een niet gefaalde naastliggende dakvloer alleen belast door eigen gewicht.
Voor ‘niet falen’ van de vloeren in de n gebouwen wordt uitgegaan van de eerste 10 jaar van de levensduur. Deze 10 jaar is een voorzichtig (conservatief) gekozen waarde voor de leeftijd van de n gebouwen, gegeven het bouwjaar van veel Nederlandse gebouwen met breedplaatvloeren.
De kans op falen van een bepaalde te analyseren vloer in de eerste 15 jaar van de levensduur wordt als volgt berekend (het |-teken in het onderstaande moet weer worden gelezen als ‘gegeven’ of ‘onder de conditie dat’ en het ∩-teken als ‘en’, T staat voor belasting door temperatuur):
Pf = P(falen beschouwde vloer in 0-15 jaar |
1 x falen Eindhoven dakvloer zonder Q en met T ∩
8 x niet falen Eindhoven verdiepingsvloer zonder Q ∩
n x niet falen gebouwen met 30 vloeren in 0-10 jaar)
Gegeven de faalkans, is de betrouwbaarheidsindex te vinden via de tabel voor de normale verdeling. Hoe meer gebouwen die goed presteren, hoe hoger de betrouwbaarheid.
In bovenstaande faalkansberekening wordt gewerkt met een referentieperiode van 15 jaar. Dit is gedaan omdat voor het afkeurniveau in NEN 8700 deze referentieperiode is voorgeschreven. We kijken dus naar een faalkans in een periode van 15 jaar volgend op de beoordeling.
Voor hetzelfde type vloer, maar kijkend naar de periode 5-20 jaar (dus onder voorwaarde dat de beschouwde vloer niet heeft gefaald in de eerste 5 jaar), wordt de kans bepaald als:
Pf = P(falen beschouwde vloer in 5-20 jaar |
1 x falen Eindhoven dakvloer zonder Q en met T ∩
8 x niet falen Eindhoven verdiepingsvloer zonder Q ∩
n x niet falen gebouwen met 30 vloeren in 0-10 jaar) ∩
1 x niet falen beschouwde vloer in 0-5 jaar)
Op dezelfde wijze kan dan worden gekeken naar een periode 10-25 jaar (dus onder voorwaarde dat de beschouwde vloer niet heeft gefaald in de eerste 10 jaar), en ook verder in de tijd.
Er wordt onderscheid gemaakt tussen normale (tussen)vloeren en dakvloeren. Bij niet geïsoleerde dakvloeren wordt extra gekeken naar effecten van opgelegde vervormingen door krimp of temperatuur.
Berekeningsuitkomsten
In [2] zijn voor alle 12 subpopulaties en leeftijden probabilistische berekeningen uitgevoerd inclusief een groot aantal variatiestudies. Voor de exacte definitie van de subpopulaties wordt verwezen naar [2]. Ter illustratie worden hieronder enkele berekeningen getoond.
In figuren 4 en 5 is het betrouwbaarheidsniveau van een te beoordelen breedplaatvloer weergegeven (uitgedrukt in een β-waarde voor een referentieperiode van 15 jaar volgend op de beoordeling conform NEN 8700 voor het afkeurniveau). Voor elk van de subpopulaties geldt een afzonderlijke lijn. In figuur 4 is de betrouwbaarheid weergegeven voor een constructie beschouwd op t = 0; met andere woorden zonder bewezen sterkte van diezelfde constructie in de tijd. In figuur 5 is de betrouwbaarheid beschouwd op t = 5 jaar, met andere woorden een bestaande constructie van minimaal 5 jaar oud. Op de horizontale as is de informatiebasis vanuit het track record gegeven. Dit geeft aan wat het effect is op de betrouwbaarheid als gevolg van het aantal succesvol presterende gebouwen met een vergelijkbare vloeropbouw. Of anders gezegd het aantal benodigde succesvolle gebouwen om een bepaalde betrouwbaarheid aan te tonen. Er is op de horizontale as van de figuren niet direct uitgegaan van een daadwerkelijk beschikbaar track record, maar er wordt van uitgegaan dat een track record met n gebouwen beschikbaar zou zijn. Uit de grafiek kan dus afgelezen worden hoeveel gebouwen er in een track record moeten zitten, om te kunnen zeggen dat de β-waarde voldoende groot is. Voor de gebouwen uit het track record (niet zijnde het gebouw dat beoordeeld wordt) wordt uitgegaan van een voorzichtig gekozen gemiddelde van 10 jaar succesvol presteren.
Doordat informatie beschikbaar is over het succesvol presteren van de eigen of andere vloerconstructies, wordt het minder waarschijnlijk dat de constructie een lage faalkans heeft; in de figuren 4 en 5 vertoont het verloop van de betrouwbaarheid een stijgende lijn met toenemende n. Met behulp van de theorie worden de schattingen van gemiddelde en standaardafwijking bijgesteld (geüpdate); het gemiddelde wordt groter, de spreiding kleiner. Bij een probabilistische berekening levert dit een kleinere faalkans op. Bij een semi-probabilistische beschouwing leidt dit tot een hogere rekenwaarde van de weerstand en daarmee een afname van de Unity Check. Ook is te zien dat de te beoordelen vloerconstructie een eigen bewezen sterkte in de tijd heeft; de waarden voor de betrouwbaarheid liggen hoger in figuur 5 dan in figuur 4. Ten slotte zijn de 12 subpopulaties zichtbaar met een duidelijk verschillend verloop van de betrouwbaarheid.
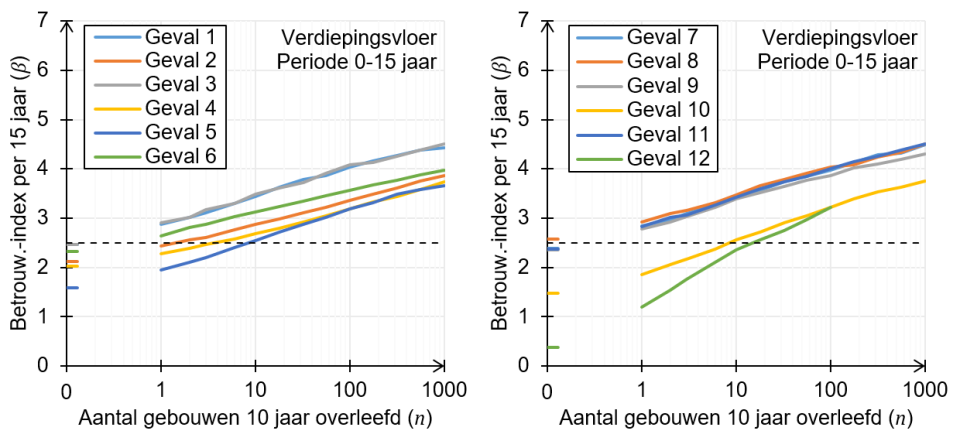
Figuur 4. Betrouwbaarheidsindex in periode 0-15 jaar versus het aantal vergelijkbare gebouwen dat 10 jaar heeft gefunctioneerd
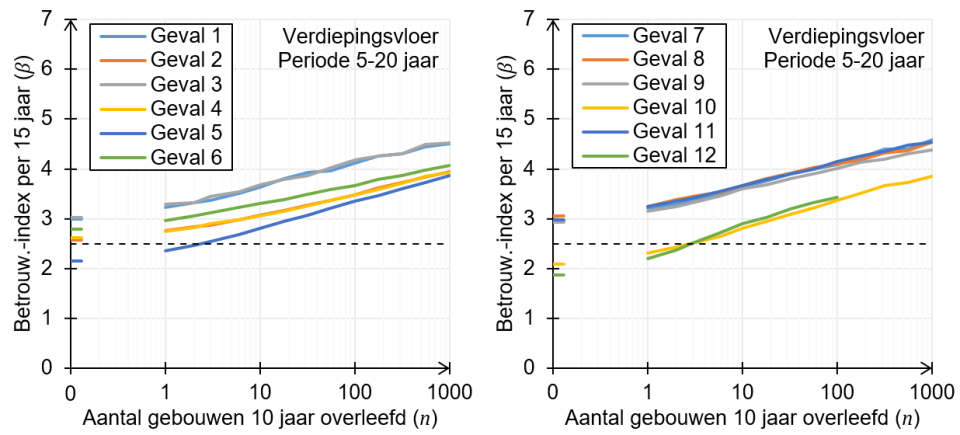
Figuur 5. Betrouwbaarheidsindex in periode 5-20 jaar versus het aantal vergelijkbare gebouwen dat 10 jaar heeft gefunctioneerd. De horizontale stippellijn geeft het afkeurniveau CC2 aan conform NEN 8700
Conclusie
TNO heeft een betrouwbaarheidsanalyse uitgevoerd voor de beoordeling van bestaande Nederlandse breedplaatvloerconstructies waarbij sprake is van primaire krachtsoverdracht (buigende momenten in het midden van een overspanning) over het constructiedetail ter plaatse van de langsnaden of langsvoegen tussen de breedplaten. Gekozen is voor het ontwikkelen van een probabilistische beoordelingsmethode. Met deze methode is het mogelijk om alle typen informatie over de constructieve sterkte en alle onzekerheden op een verantwoorde wijze mee te nemen en de vloeren direct te toetsen aan de in de vigerende regelgeving vereiste betrouwbaarheid. Zowel informatie uit laboratoriumproeven over het gedrag van de naad en informatie uit het track record van bestaande vloerconstructies is verwerkt. Het track record bevat het falen van de dakvloer bij de parkeergarage van Eindhoven Airport, evenals het niet falen (overleven) van vloeren van gebouwen met breedplaatvloeren onder opgetreden gebruiksbelastingen en proefbelastingen.
Conclusie: In aanleg kunnen grote vraagtekens worden geplaatst bij de constructieve veiligheid van breedplaatvloeren gebouwd tot 2017 waarbij primaire krachtsafdracht plaats moet vinden bij de langsvoeg. Dit is het gevolg van de rekenkundig gezien onvoldoende detaillering ter plaatse van de langsvoeg. Door combinatie van de rekenmodellen, de uitkomsten van laboratoriumproeven en de bewezen sterkte analyse kan echter worden geconcludeerd dat voor bepaalde gebouwtypologieën de vloeren toch voldoende betrouwbaar zijn.
Voor de conclusies op niveau van de verschillende subpopulaties wordt verwezen naar [2]]. Bijzondere aandacht is daarin gevraagd voor direct door zonlicht bestraalde dakvloeren en grote overspanningen (10-15m); deze voldoen na analyse niet aan de betrouwbaarheidseis voor CC2 uit NEN 8700 en de betrouwbaarheid is zeer laag.
Literatuur
- Wijte, S., & Dieteren, G., Rekenregels beoordeling bestaande breedplaatvloeren. Cement 2019/4.
- Steenbergen, R., Dieteren, G., Vries, R. de, Borsje, H., Vrouwenvelder, T., & Wijte, S. TNO-2022-R10122 Probabilistische kwantificering van de veiligheid van bestaande breedplaatvloeren. Delft: TNO, 2022.
- Wijte, S., & Dieteren, G., Vereenvoudigde beoordelingsprocedure bestaande breedplaatvloeren. Cement 2024/4.



Reacties