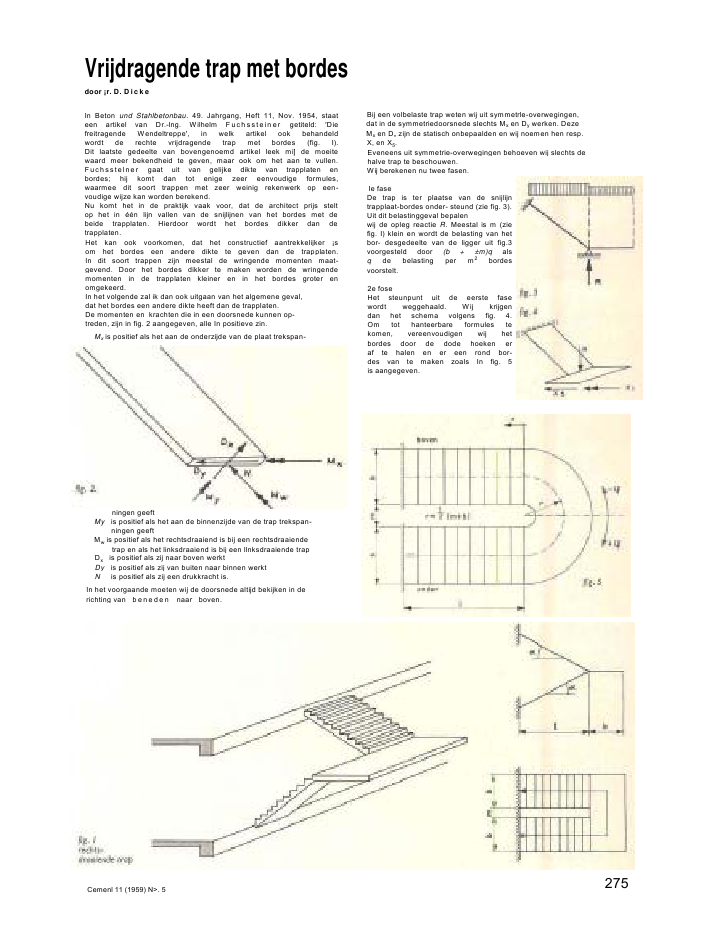
Vrijdragende trap met bordesdoor ?r. D. D i ck eIn Beton und Stahlbetonbau. 49. Jahrgang, Heft 11, Nov. 1954, staateen artikel van Dr.-lng. Wilhelm Fuchssteiner getiteld: 'Diefreitragende Wendeltreppe', in welk artikel ook behandeldwordt de rechte vrijdragende trap met bordes (fig. I).Dit laatste gedeelte van bovengenoemd artikel leek mi] de moeitewaard meer bekendheid te geven, maar ook om het aan te vullen.Fuchsstelner gaat uit van gelijke dikte van trapplaten enbordes; hij komt dan tot enige zeer eenvoudige formules,waarmee dit soort trappen met zeer weinig rekenwerk op een-voudige wijze kan worden berekend.Nu komt het in de praktijk vaak voor, dat de architect prijs steltop het in ??n lijn vallen van de snijlijnen van het bordes met debeide trapplaten. Hierdoor wordt het bordes dikker dan detrapplaten.Het kan ook voorkomen, dat het constructief aantrekkelijker ?som het bordes een andere dikte te geven dan de trapplaten.In dit soort trappen zijn meestal de wringende momenten maat-gevend. Door het bordes dikker te maken worden de wringendemomenten in de trapplaten kleiner en in het bordes groter enomgekeerd.In het volgende zal ik dan ook uitgaan van het algemene geval,dat het bordes een andere dikte heeft dan de trapplaten.De momenten en krachten die in een doorsnede kunnen op-treden, zijn in fig. 2 aangegeven, alle In positieve zin.Mx is positief als het aan de onderzijde van de plaat trekspan-ningen geeftMy is positief als het aan de binnenzijde van de trap trekspan-ningen geeftMw is positief als het rechtsdraaiend is bij een rechtsdraaiendetrap en als het linksdraaiend is bij een llnksdraaiende trapDx is positief als zij naar boven werktDy is positief als zij van buiten naar binnen werktN is positief als zij een drukkracht is.In het voorgaande moeten wij de doorsnede altijd bekijken in derichting van bene den naar boven.Bij een volbelaste trap weten wij uit symmetrle-overwegingen,dat in de symmetriedoorsnede slechts Mx en Dy werken. DezeMx en D,, zijn de statisch onbepaalden en wij noemen hen resp.X, en X5.Eveneens uit symmetrie-overwegingen behoeven wij slechts dehalve trap te beschouwen.Wij berekenen nu twee fasen.Ie faseDe trap is ter plaatse van de snijlijntrapplaat-bordes onder- steund (zie fig. 3).Uit dit belastinggeval bepalenwij de opleg reactie R. Meestal is m (ziefig. I) klein en wordt de belasting van hetbor- desgedeelte van de ligger uit fig.3voorgesteld door (b + ?m)q alsq de belasting per m2bordesvoorstelt.2e foseHet steunpunt uit de eerste fasewordt weggehaald. Wij krijgendan het schema volgens fig. 4.Om tot hanteerbare formules tekomen, vereenvoudigen wij hetbordes door de dode hoeken eraf te halen en er een rond bor-des van te maken zoals In fig. 5is aangegeven.Cemenl 11 (1959) N>. 5 275In deze fase kunnen de onbekenden X, en Xs met de arbeids-methode worden berekend. Om compleet te zijn, zal ik in hetkort deze arbeidsmethode toelichten.Vormveranderingen door dwarskrachten en normaalkrachtenworden verwaarloosd.De vormveranderingsarbeid isIn debovenste (onderste) trapplaat is:Hoewel principieel niet moeilijk, is het uitcijferen van de factorenS toch nog tijdrovend. Bovendien zal vaak blijken, dat de gekozendikten niet goed of voor verbetering vatbaar zijn en dan moetweer opnieuw worden gecijferd.276 Comem 11 (19S9) Nt. 3Al dit cijferwerk ?s te vereenvoudigen door al die termen, dieslechts afhankelijk zijn van de vaste waarden , r en /, vooruitvast te stellen. Deze factoren zijn voor elke herhaling van deberekening gelijk.Slechts de stijfheden ?x, Iy en /w zijn veranderlijk.Door alle factoren te vermenigvuldigen met ?(, veranderenwij niets aan X, en Xs.De met de dikten vari?rende factoren zijn dan:Bij iedere herhaling van de berekening moeten bovenstaandefactoren e. f, g en h opnieuw worden bepaald, wat overigensweinig cijferwerk vraagt.Onveranderlijk zijnde volgende factoren :Hiermee zijn in elke doorsnede de momenten en krachtenbekend. Op de waarden uit de Ie fase superponeren wij dewaarden door fi veroorzaakt (2efase):In het bordes:Wat ??k onze belangstelling heeft, is de overgang van de trapnaar de vloer of naar een fundering. In het voorgaande beschouw-den wij doorsneden loodrecht op de trapplaat. Bij de overgangtrap-vloer hebben wij meer aan werking in de doorsnede lood-recht op de vloer.In de verticale doorsnede van de overgang trap-vloer (x=/) is:Mx = Mx ~DX = N sina + Dx cosaMy = A1w sina + My cosa Dy = DyMw = Mw cosa- My sina N = N cos a-Dx sin aCement 11 (1959) Nr. ? 277De veranderlijke factoren zijn :De verticale doorsnede van ceze aansluiting heeft nu:Mx =-1430 kgmMy = + 1070 + 4 270 = +5 340 kgmMw = + 1440-3 200 = - I '60 kgmDx =-4700-l230 = -5'>30kgDy =0? =-6260 + 920 = -5340kgControle (fig. 10)Verticaal evenwicht:2 3920 + 4000 = 2?7 840 + 4 000 = 2 D^ = 2 5 930klopt!Momenten om verticale as :5 340 2,00 = 2/v? = 2x5 340klopt!278 Cement 11 (1959) Nr. 3Dus totaal uit leen 2efase:Mx =-500- 110 = -610 kgm Dx=-I060kgMy = + 8 530 kgm Dy = 0Mw=+760kgm N =-9890 kgIn de verticale doorsnede is nu :Mx =-610 kgmMy = + 460 + 6 820 = + 7 280 kgmMw= +610-5 120 = -4510 kgmDx = - 5 930 - 850 = - 6 780 kj.mDy = 0? =-7910 + 640 =-7270 kgControle (fig. 12)Verticaal evenwicht:2 3920 + 5 720 = 2DX7 840 + 5 720 = 2 6 78013 560= 13 560 klopt!Momenten om verticale as:7 270 2,00 = 2My = 2 7 280 klopt!Momenten om horizontale as:2 3920 1,20 + 5720 3,15 =7JX3,60 + 2MX9 410 + 17 980 = 26 200+ I 22027 390 = 27 420 klopt!Met behulp van deze gegevens kunnen nu overal in de constructiede spanningen worden gecontrokerd en de wapening bepaald.Men zie hiertoe de genoemde publikatie van Dr.-lng. Fuchs-steiner, waarin dit zeer uitvoerij wordt behandeld.Het voorgaande gold uitsluitend voor symmetrische trappen.Zodra de beide trapplaten ongelij < van lengte worden, word", deberekening veel bewerkelijker, d.iar dan 6 statisch onbepaaldenmoeten worden bepaald en men do invloed van het bordes andersmoet interpreteren.Met de hulp van het voorgaande t iedt dit geen bijzondere moei-lijkheden meer, maar het vergt wel veel geduld.Cement 11 (1959) Ni. 3 279