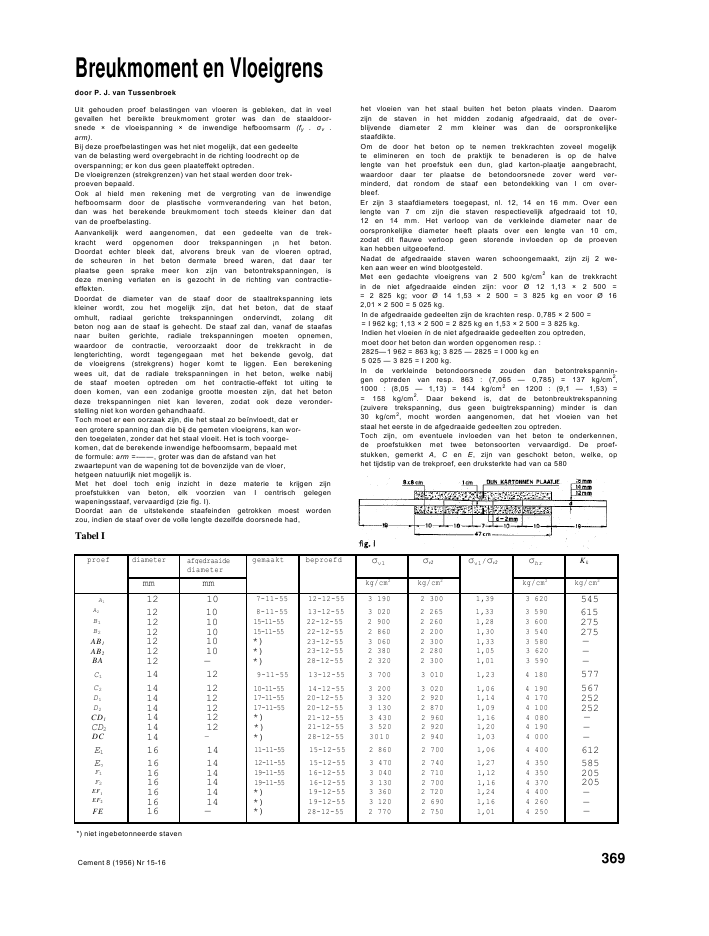
Breukmoment en Vloeigrensdoor P. J. van TussenbroekUit gehouden proef belastingen van vloeren is gebleken, dat in veelgevallen het bereikte breukmoment groter was dan de staaldoor-snede ? de vloeispanning ? de inwendige hefboomsarm (fy . .arm).Bij deze proefbelastingen was het niet mogelijk, dat een gedeeltevan de belasting werd overgebracht in de richting loodrecht op deoverspanning; er kon dus geen plaateffekt optreden.De vloeigrenzen (strekgrenzen) van het staal werden door trek-proeven bepaald.Ook al hield men rekening met de vergroting van de inwendigehefboomsarm door de plastische vormverandering van het beton,dan was het berekende breukmoment toch steeds kleiner dan datvan de proefbelasting.Aanvankelijk werd aangenomen, dat een gedeelte van de trek-kracht werd opgenomen door trekspanningen ?n het beton.Doordat echter bleek dat, alvorens breuk van de vloeren optrad,de scheuren in het beton dermate breed waren, dat daar terplaatse geen sprake meer kon zijn van betontrekspanningen, isdeze mening verlaten en is gezocht in de richting van contractie-effekten.Doordat de diameter van de staaf door de staaltrekspanning ietskleiner wordt, zou het mogelijk zijn, dat het beton, dat de staafomhult, radiaal gerichte trekspanningen ondervindt, zolang ditbeton nog aan de staaf is gehecht. De staaf zal dan, vanaf de staafasnaar buiten gerichte, radiale trekspanningen moeten opnemen,waardoor de contractie, veroorzaakt door de trekkracht in delengterichting, wordt tegengegaan met het bekende gevolg, datde vloeigrens (strekgrens) hoger komt te liggen. Een berekeningwees uit, dat de radiale trekspanningen in het beton, welke nabijde staaf moeten optreden om het contractie-effekt tot uiting tedoen komen, van een zodanige grootte moesten zijn, dat het betondeze trekspanningen niet kan leveren, zodat ook deze veronder-stelling niet kon worden gehandhaafd.Toch moet er een oorzaak zijn, die het staal zo be?nvloedt, dat ereen grotere spanning dan die bij de gemeten vloeigrens, kan wor-den toegelaten, zonder dat het staal vloeit. Het is toch voorge-komen, dat de berekende inwendige hefboomsarm, bepaald metde formule: arm =-----, groter was dan de afstand van hetzwaartepunt van de wapening tot de bovenzijde van de vloer,hetgeen natuurlijk niet mogelijk is.Met het doel toch enig inzicht in deze materie te krijgen zijnproefstukken van beton, elk voorzien van I centrisch gelegenwapeningsstaaf, vervaardigd (zie fig. I).Doordat aan de uitstekende staafeinden getrokken moest wordenzou, indien de staaf over de volle lengte dezelfde doorsnede had,Tabel Ihet vloeien van het staal buiten het beton plaats vinden. Daaromzijn de staven in het midden zodanig afgedraaid, dat de over-blijvende diameter 2 mm kleiner was dan de oorspronkelijkestaafdikte.Om de door het beton op te nemen trekkrachten zoveel mogelijkte elimineren en toch de praktijk te benaderen is op de halvelengte van het proefstuk een dun, glad karton-plaatje aangebracht,waardoor daar ter plaatse de betondoorsnede zover werd ver-minderd, dat rondom de staaf een betondekking van I cm over-bleef.Er zijn 3 staafdiameters toegepast, nl. 12, 14 en 16 mm. Over eenlengte van 7 cm zijn die staven respectievelijk afgedraaid tot 10,12 en 14 mm. Het verloop van de verkleinde diameter naar deoorspronkelijke diameter heeft plaats over een lengte van 10 cm,zodat dit flauwe verloop geen storende invloeden op de proevenkan hebben uitgeoefend.Nadat de afgedraaide staven waren schoongemaakt, zijn zij 2 we-ken aan weer en wind blootgesteld.Met een gedachte vloeigrens van 2 500 kg/cm2kan de trekkrachtin de niet afgedraaide einden zijn: voor ? 12 1,13 ? 2 500 == 2 825 kg; voor ? 14 1,53 ? 2 500 = 3 825 kg en voor ? 162,01 ? 2 500 = 5 025 kg.In de afgedraaide gedeelten zijn de krachten resp. 0,785 ? 2 500 == I 962 kg; 1,13 ? 2 500 = 2 825 kg en 1,53 ? 2 500 = 3 825 kg.Indien het vloeien ?n de niet afgedraaide gedeelten zou optreden,moet door het beton dan worden opgenomen resp. :2825--1 962 = 863 kg; 3 825 -- 2825 = I 000 kg en5 025 -- 3 825 = I 200 kg.In de verkleinde betondoorsnede zouden dan betontrekspannin-gen optreden van resp. 863 : (7,065 -- 0,785) = 137 kg/cm2,1000 : (8,05 -- 1,13) = 144 kg/cm2en 1200 : (9,1 -- 1,53) == 158 kg/cm2. Daar bekend is, dat de betonbreuktrekspanning(zuivere trekspanning, dus geen buigtrekspanning) minder is dan30 kg/cm2, mocht worden aangenomen, dat het vloeien van hetstaal het eerste in de afgedraaide gedeelten zou optreden.Toch zijn, om eventuele invloeden van het beton te onderkennen,de proefstukken met twee betonsoorten vervaardigd. De proef-stukken, gemerkt A, C en E, zijn van geschokt beton, welke, ophet tijdstip van de trekproef, een druksterkte had van ca 580proef diameter afgedraaidediametergemaakt beproefd 1 v2 1/v2 hr Kkmm mm kg/cm2kg/cm2kg/cm2kg/cm2A1 12 10 7-11-55 12-12-55 3 190 2 300 1,39 3 620 545A2 12 10 8-11-55 13-12-55 3 020 2 265 1,33 3 590 615B1 12 10 15-11-55 22-12-55 2 900 2 260 1,28 3 600 275B2 12 10 15-11-55 22-12-55 2 860 2 200 1,30 3 540 275AB1 12 10 *) 23-12-55 3 060 2 300 1,33 3 580 --AB2 12 10 *) 23-12-55 2 380 2 280 1,05 3 620 --BA 12 -- *) 28-12-55 2 320 2 300 1,01 3 590 --C1 14 12 9-11-55 13-12-55 3 700 3 010 1,23 4 180 577C2 14 12 10-11-55 14-12-55 3 200 3 020 1,06 4 190 567D1 14 12 17-11-55 20-12-55 3 320 2 920 1,14 4 170 252D2 14 12 17-11-55 20-12-55 3 130 2 870 1,09 4 100 252CD1 14 12 *) 21-12-55 3 430 2 960 1,16 4 080 --CD2 14 12 *) 21-12-55 3 520 2 920 1,20 4 190 --DC 14 -- *) 28-12-55 3010 2 940 1,03 4 000 --E1 16 14 11-11-55 15-12-55 2 860 2 700 1,06 4 400 612E2 16 14 12-11-55 15-12-55 3 470 2 740 1,27 4 350 585F1 16 14 19-11-55 16-12-55 3 040 2 710 1,12 4 350 205F2 16 14 19-11-55 16-12-55 3 130 2 700 1,16 4 370 205EF1 16 14 *) 19-12-55 3 360 2 720 1,24 4 400 --EF2 16 14 *) 19-12-55 3 120 2 690 1,16 4 260 --FE 16 -- *) 28-12-55 2 770 2 750 1,01 4 250 --*) niet ingebetonneerde stavenCement 8 (1956) Nr 15-16 369kg/cm2, vervaardigd door de N.V. Schokindustrie te Zwijndrecht,waarvoor hier nog mijn dank voor de medewerking.De overige proefstukken, gemerkt B, D en F zijn van gebruikelijkbeton met een druksterkte van ca 240 kg/cm2.Ook zijn afgedraaide, niet ingebetonneerde, staven aan een trek-proef onderworpen : AB, CD en EF.Al deze proeven zijn in tweevoud uitgevoerd.Ten slotte zijn nog niet afgedraaide staven, BA, DC en FE, beproefd,echter in enkelvoud, daar van dezelfde diameter en staaf geenstaal meer aanwezig was.Voor het verrichten van de trekproeven mocht gebruik wordengemaakt van de 50 tons trekbank in het laboratorium van deMiddelbare Technische School te Rotterdam.Ook voor de medewerking van die zijde mijn dank.Bij de staven ? 12 mm werd de trekkracht opgevoerd met 20 kgper minuut, terwijl de aanvangstrekkracht 500 kg bedroeg. Bij destaven ? 14 mm waren deze waarden 33 kg en 800 kg en bij destaven ? 16 mm resp. 40 kg en 1000 kg.De resultaten van de beproevingen zijn verzameld in tabel I.Uit deze tabel blijkt, dat voor de staven ? 12 de eerste vloeigrensvan de afgedraaide staven gemiddeld 3 105 kg/cm2is voor A, en2 880 kg/cm2voor B. Er is dus een verschil tussen deze vloeigren-zen, wat veroorzaakt kan zijn doordat de proefstukken A van ge-schokt beton en de stukken B van gewoon beton zijn vervaardigd.Van de niet ingebetonneerde, maar wel afgedraaide staven ABmoet AB2 als een uitschieter worden gezien, waarover later meerwordt gezegd.De vloeigrens van de staaf ABI, betrokken op de doorsnede van? 10 mm, komt nagenoeg overeen met de gemiddelde vloeigrensvan de staven A en B, waaruit de conclusie kan worden getrokken,dat het beton geen, of slechts een zeer geringe, invloed uitoefentop de Ie vloeigrens van ingebetonneerde staven.De niet afgedraaide staaf BA heeft een vloeigrens van 2 320 kg/cm2,betrokken op een doorsnede van ? 12 mm en een 2e vloeigrensvan 2 300 kg/cm2, dus nagenoeg gelijk aan de le vloeigrens.Deze vloeigrens komt in grote trekken overeen met de 2e vloei-grens van de staven A en B.Bij de staven ? 14 mm zijn de gemiddelde le vloeigrenzen van Cen D resp. 3 450 kg/cm2en 3 225 kg/cm2. De afgedraaide, niet in-gebetonneerde staven CD hebben een eerste vloeigrens, die zelfsjets groter is dan de gemiddelde van C en D.Bij de niet afgedraaide staaf DC is er weer weinig verschil tussende le en 2e vloeigrens en komt de eerste vloeigrens overeen metde 2e vloeigrens van C, D en CD.Bij de staven ? 16 mm is er niet veel onderscheid tussen E en F enzelfs niet met EF. Ook hier is bij de staaf FE de le en 2e vloeigrenspraktisch gelijk en komt deze vloeigrens overeen met de 2e vloei-grens van de afgedraaide staven.Uit het geheel blijkt, dat het beton niet veel invloed heeft gehadop de vloeigrenzen van het staal.Dat de, al of niet ingebetonneerde, afgedraaide staven een veelhogere eerste vloeigrens hebben dan de niet afgedraaide staven geefteen aanwijzing, dat gezocht moet worden, hoe dit verschil bij detrekproef optreedt.Bij een trekproef worden de staven aan de einden vastgehoudendoor de zgn. 'inspanbekken'. Deze oefenen op de staaf radiaal ge-richte drukkrachten uit, waardoor de contractie, die wordt ver-oorzaakt door de trekkracht in de richting van de staafas, wordtvergroot, zodat dus een lagere vloeigrens ontstaat. Hierdoor isook de uitschieter, staaf AB2, te verklaren, daar 1,13 ? 2 280 == 2 570 kg en 2 570 : 0,785 = 3270 kg/cm2.Bij deze staaf is de invloed van de drukkrachten door de inspan-bekken dus wel zeer groot geweest. In feite worden dus de vloei-grenzen, zoals die worden bepaald op niet afgedraaide staven, be-invloed door het 'bek-effect'.In een gewapend-betonconstructie heeft de wapening g??n nade-lige invloed van dit bek-effect en zullen de werkelijke vloeigrenzenoptreden, zoals die hiervoor zijn bepaald op de, in het midden,afgedraaide staven. Wel is het opmerkelijk, dat (zie tabel I) deinvloed van de inspanbekken bij de kleine diameters groter is danbij de dikkere staven; voor de staven A en B is dit rond 30% envoor de overige staven rond 14%. Nu hebben dunne staven overhet algemeen reeds een hogere, op de conventionele manier be-paalde, vloeigrens dan de dikkere staven. Zoals uit bovenstaandeproeven blijkt, zal in werkelijkheid dit verschil nog groter zijn.Hieruit is wellicht te verklaren, dat bij een laag wapeningspercen-tage (dunne staven) het gevonden breukmoment uit een proef-belasting meer afwijkt van het berekende breukmoment dan bijtoepassing van een groot wapeningspercentage (dikke staven).Uit het voorgaande mag niet de conclusie worden getrokken dat,wanneer bij een trekproef een vloeigrens gevonden wordt die be-neden de voorgeschreven vloeigrens ligt, het staal toch goed is,daar in de toegelaten spanningen reeds rekening is gehouden metgunstige faktoren van het staal. Met een toegelaten spanning van1200 kg/cm2resp. 1400 kg/cm2zou het anders nooit mogelijk zijneen 2?-voudige veiligheid van de betonconstructie te bereiken.Wel geeft het voorgaande een verklaring, hoe het mogelijk is, datde berekende inwendige hefboomsarm uit arm = -z groter isdan de afstand vanaf het zwaartepunt van de wapening tot boven-kant plaat.In fig. 2 is het spanning-rekdiagram getekend van de afgedraaide,niet ingebetonneerde, staaf ABI. Hieruit blijkt, dat de afstand /-///ongeveer 3,5 maal ) /-// is. Het is dan ook de vraag of, ten opzichtevan het staal, nog een voldoende waarschuwing tegen plotselingebreuk van de betonconstructie mag worden verwacht.Bij statisch-onbepaalde constructies is deze waarschuwing zekeraanwezig, maar deze komt voort uit de berekening van de mo-menten die, rekening houdende met afwisselende belasting van develderi, een reserve geven.Ik ben mij bewust, dat het gehele probleem door de hier beschre-ven proeven niet is opgelost, daar er nog wel meer faktoren eenrol zullen spelen, zoals bij gewapend beton altijd het geval is. Tochhoop ik dat met deze bijdrage een stap in de goede richting is ge-daan.Moment of Failure and Limit of StretchingStrainby P. ]. van TussenbroekIt appears from loading tests on floors in manyinstances that the moment of failure obtained isgreater than the cross-section of the rods, stret-ching strain, and interior lever arm. There iscertainly no slab-effect. The limits of stretchingstrain (tensile limits) of the steel have been deter-mined by tensioning tests. The calculated momentof failure is always smaller than that of the loadingtest, even if one takes into account the enlarge-ment of the interior lever arm as a consequence ofthe plastic form changes of the concrete. It wasoriginally assumed that part of the tensile strengthwas absorbed by tensile strains in the concrete;this, however, is not the case. Later, attemptswere made to locate the cause in the contractioneffects. A calculation has shown that this assump-tion cannot be correct.The author describes tests taken by him withconcrete members that have one centric rein-forcing rod with a smaller cross-section in themiddle so that the flow of the steel takes place inthe concrete. The results have been assembled ina table.370Moment de rupture et limite de tractionpar P. J. van TussenbroekLes charges d'essai de planchers ont montr? dansbien des cas que le moment de rupture est plusgrand que diam?tre de barre, tension de tractionet bras du levier interne. Il ne saurait ?tre questiond'un effet de plaque. Les limites de traction del'acier sont d?termin?es ? l'aide d'essais detraction. Le moment de rupture est toujours pluspetit que celui de la charge d'essai, m?me si ontient compte de l'agrandissement du bras du levierinterne par la d?formation plastique du b?ton. Onsupposait au d?but qu'une partie de la force detraction est absorb?e par des tensions de tractiondans le b?ton, ce qui n'est cependant pas le cas.On a ?tudi? ensuite la possibilit? d'effets decontraction. Un calcul a montr? que cette suppo-sition ne peut ?tre juste.L'auteur d?crit des essais faits par lui sur desmorceaux de b?ton avec une barre d'armementcentrale ayant au milieu un diam?tre plus petit,de sorte que l'etirement de l'acier a lieu dans leb?ton. Le tableau indique les r?sultats.Bruchmoment und Fliesgrenzevon P. J, TussenbroekIn vielen F?llen geht aus Probebelastungen vonDeckenkonstruktionen hervor, dass das erzielteBruchmoment gr?sser ist als das Produkt ausStabq?erschnitt mal Fliessspannung mal Abstandzwischen Druckmittelpunkt und Armierungs-schwerpunkt (innerer Hebelsarm). Von Platten-wirkung kann keine Rede sein. Die Fliessgrenzedes Stahles ist mit Hilfe von Zugproben bestimmt.Das berechnete Bruchmoment ist nun stets kleinerals das unter der Bruchbelastung auftretende,selbst dann, wenn mit der Vergr?sserung desinneren Hebelsarmes zufolge der plastischenForm?nderung des Betons gerechnet wird.Urspr?nglich wurde angenommen, dass ein Teilder Zugkraft als Zugspannungen im Beton auf-genommen wird, was aber nicht der Fall ist.Hierauf wurde die L?sung in der Richtung nachKontraktionswirkungen gesucht. Eine Berechnunghat ausgewiesen, dass diese Annahme nichtrichtig sein kann. Der Verfasser beschreibt vonihm selbst vorgenommenen Versuche mit Beton-probek?rpern, armiert mit einem zentrisch ange-brachten Armierungsstab, der im mittleren Teileinen kleineren Durchmesser hatte, sodassFliessen des Armierungsstahles stattfinden musste.Die Resultate sind in einer Tabelle zusammen-gefasst.Cement 8 (1956) Nr 15-16