Een verlopende hoogte in een constructie heeft effect op de grootte van de inwendige dwarskracht. Dat kan leiden tot onverwachte zaken, waarmee in de praktijk niet altijd goed rekening wordt gehouden.
46? CEMENT 6 2024
EFFECTEN OP
DWARSKRACHT IN
CONSTRUCTIES
MET VERLOPENDE
HOOGTE
Een verlopende hoogte in een constructie heeft
effect op de grootte van de inwendige
dwarskracht. Dat kan leiden tot onverwachte
zaken, waarmee in de praktijk niet altijd goed
rekening wordt gehouden.
Iedere constructeur kent wel artikel 6.2.1(2) uit
NEN-EN 1992-1-1 (EC2), waarin staat aangegeven
dat de dwarskrachtweerstand van een element met
dwarskrachtwapening gelijk is aan (formule 6.1):
V
Rd = V Rd,s + V ccd + V td
Voor elementen met verlopende hoogte wordt deze
vergelijking toegelicht met figuur 6.2 uit Eurocode 2
(fig. 1). Feitelijk komt het erop neer dat de voor dwars-
kracht benodigde hoeveelheid beugels in een ligger
met verlopende hoogte mag worden gereduceerd tot:
V
Rd,s = V Rd - V ccd - V td
Doorsneden met dwarskrachtwapening
Om een beter beeld te krijgen van wat er met een
ligger met verlopende hoogte gebeurt, wordt een vak -
werkanalogie beschouwd. Daarbij wordt uitgegaan
van het in figuur 2 weergegeven vakwerk van een aan
één zijde ingeklemde ligger die aan het vrije uiteinde
RUBRIEK NORMBESEF
Dit is het zevende artikel in de
Cement-rubriek Normbesef.
In deze rubriek kunnen lezers
onduidelijkheden in de construc -
teurspraktijk, bijvoorbeeld in de
regelgeving, aankaarten.
Let wel: Hoewel de artikelen
worden beoordeeld door ex -
perts, betreft het de persoonlijke
interpretatie van de auteur. Aan
de inhoud kunnen dan ook geen
rechten worden ontleend. De
artikelen geven ook niet altijd
een antwoord of oplossing.
Het doel van de rubriek is de
sector te informeren over on-
duidelijkheden en daarmee een
discussie op gang brengen. Dit
kan leerzaam zijn, zo meent de
redactie van Cement. Uiteraard
voor de normcommissie, maar
ook voor collega-constructeurs.
Het uiteindelijke doel van de
rubriek is meer duidelijkheid
voor iedereen en in sommige
gevallen misschien zelfs betere
normen.
Een uitgebreidere toelichting
op de rubriek staat in het artikel
'Nieuwe rubriek over normen:
Normbesef' op Cementonline.
Heb je zelf ook een onderwerp
voor deze rubriek, neem dan
contact op met Jacques Linssen,
j.linssen@aeneas.nl. Publicatie
kan eventueel anoniem.
Figuur 1. Dwarskrachtcomponent voor
elementen met verlopende hoogte
(figuur 6.2 uit EC2)
Normbesef (7)
CEMENT 6 2024 ?47
auteur
IR. HANS GALJAARD
wordt belast door een moment M en dwarskracht V.
Een positief moment en dwarskracht komen hierbij
overeen met de aangegeven richtingen.
De lengte van de ligger is l, de hoogte links h
l en rechts
h
r. De helling van de onderrandstaaf is ? = 15°, en voor
de eenvoud die van de diagonalen ? = 45°, en van de
bovenrandstaaf
? = 0°. De relatie tussen h l en h r volgt
dus uit h
l = h r + l · tan ?.
Als wordt aangenomen dat h
r = 1 m, dan geldt voor l =
9,263 m en voor h
l = 3,482 m op een heel aantal velden
uit te komen.
Voor deze afleiding zijn een aantal goniometrische
relaties gebruikt. De horizontaal gemeten lengte van
één vak van het vakwerk volgt uit:
()
= v vr sin cos
sin
lh
() = + DL V cos
sin
FF
= +OL OR DR cos cos
F FF
= BL BR DL cos cos
F FF
( )
= V DR sin
cos
FF
?? ?? = = = ?? ??
?? ??
h h
2
2 2
M yy
_h _h
2 2
2
2
M y y DxDy M DxDy M DxDy Vb dyy b dy
h
I Ihh
= = \fit
in \fit M \fitM DxDy VVVV h
= = \fit
in \fit 3, \b31 0, 268 0
1
V
VV
red = tan M
QQ h
met h vr de hoogte van het beschouwde vak aan de
rechterzijde. Voor de hoogtetoename geldt
?h = l
v · (tan ? + tan ?)
De krachten in de verticalen van dit vakwerk worden be-
paald voor een dwarskracht V = 10 kN of een moment
M = 10 kNm. De resultaten zijn weergegeven in tabel 1.
In het vakwerk gelden de volgende evenwichtsrelaties
(fig. 3): ?
()
= v vr sin cos
sin
lh
() = + DL V cos sin FF
= +OL OR DR cos cos
F FF
= BL BR DL cos cos
F FF
( )
= V DR sin
cos
FF
?? ?? = = = ?? ??
?? ??
h h
2
2 2
M yy
_h _h
2 2
2
2
M y y DxDy M DxDy M DxDy Vb dyy b dy
h
I Ihh
= = \fit
in \fit M \fitM DxDy VVVV h
= = \fit
in \fit 3, \b31 0, 268 0
1
V
VV
red = tan M
QQ h
?
()
= v vr sin cos
sin
lh
() = + DL V cos sin
FF
= +OL OR DR cos cos F FF
= BL BR DL cos cos
F FF
( )
= V DR sin
cos
FF
?? ?? = = = ?? ??
?? ??
h h
2
2 2
M yy
_h _h
2 2
2
2
M y y DxDy M DxDy M DxDy Vb dyy b dy
h
I Ihh
= = \fit
in \fit M \fitM DxDy VVVV h
= = \fit
in \fit 3, \b31 0, 268 0
1
V
VV
red = tan M
QQ h
?
()
= v vr sin cos
sin
lh
() = + DL V cos sin
FF
= +OL OR DR cos cos
F FF
= BL BR DL cos cos F FF
( )
= V DR sin
cos
FF
?? ?? = = = ?? ??
?? ??
h h
2
2 2
M yy
_h _h
2 2
2
2
M y y DxDy M DxDy M DxDy Vb dyy b dy
h
I Ihh
= = \fit
in \fit M \fitM DxDy VVVV h
= = \fit
in \fit 3, \b31 0, 268 0
1
V
VV
red = tan M
QQ h
?
()
= v vr sin cos
sin
lh
() = + DL V cos sin
FF
= +OL OR DR cos cos
F FF
= BL BR DL cos cos
F FF
( )
= V DR sin
cos
FF
?? ?? = = = ?? ??
?? ??
h h
2
2 2
M yy
_h _h
2 2
2
2
M y y DxDy M DxDy M DxDy Vb dyy b dy
h
I Ihh
= = \fit
in \fit M \fitM DxDy VVVV h
= = \fit
in \fit 3, \b31 0, 268 0
1
V
VV
red = tan M
QQ h
Het, schijnbaar opvallende, resultaat is dus dat de
inwendige dwarskracht in de ligger afneemt terwijl de
uitwendige dwarskracht constant blijft. Verder valt op
dat door het moment een tegengestelde dwarskracht
ontstaat.
Bij het eveneens in tabel 1 weergegeven moment M =
37,32 kNm blijkt de som van de inwendige dwarskracht
door de uitgeoefende dwarskracht en moment zelfs nul
te worden.
Dit is op zich niet zo vreemd ? het snijpunt van de
boven- en onderrandstaaf bevindt zich 1 m / tan ? =
1 m / tan 15° = 3,73 m rechts van het vakwerk. Een
Figuur 2. Vakwerk van ligger met verlopende hoogte
Figuur 3. Evenwichtsrelaties in vakwerk
Tabel 1 Uitwerking krachten in vakwerk in kN
Staaf V = 10 kNM = 10 kNmM = 37,32 kNm
1 ? 6 10-2.68-10
2 ? 7 7.32-1.96-7.32
3 ? 8 5.36-1.44-5.36
4 ? 9 3.92-1.05-3.92
5-Oct 2.87-0.77-2.87
48? CEMENT 6 2024
moment M = 37,32 kNm komt dus overeen met een
dwarskracht die exact in het snijpunt van de boven- en
onderrand aangrijpt, en dus geheel kan worden opge-
nomen door de normaalkrachten in deze staven.
In figuur 4 wordt weergegeven wat dit betekent. Het
moment kan worden gezien als een dwarskracht die
met een bepaalde excentriciteit wordt uitgeoefend.
Met toenemende excentriciteit neemt de inwendige
(niet de uitwendige) dwarskracht af totdat deze nul
wordt, als de excentrische dwarskracht samenvalt met
het snijpunt van de boven- en onderrand. Wanneer
de excentriciteit nog groter wordt, dan zal de inwen-
dige dwarskracht een aan de uitwendige dwarskracht
tegengesteld teken krijgen. Bij een moment dat in
verhouding groot is ten opzichte van de dwarskracht,
kan de inwendige dwarskracht niet alleen van teken
omslaan, maar in absolute zin zelfs groter worden dan
de uitwendige dwarskracht. Wanneer in plaats van ? = 15° wordt aangehouden
? = 0° en
? = 15°, verandert wel de geometrie en
krachtswerking in het vakwerk, maar bij een moment
M = 37,32 kNm blijft de inwendige dwarskracht nog
steeds gelijk aan nul!
Lineair elastische doorsneden
Nu kan de vraag worden gesteld hoe het dan zit met
een nog volledig elastische (ongescheurde) ligger.
Hiertoe wordt uitgegaan van een uitkragende ligger
met constante breedte en verlopende hoogte (fig. 5).
Om de afleiding wat eenvoudiger te houden krijgen
boven- en onderrand dezelfde helling zodat geldt
tan ? + tan
? = tan 15° => ? = ? = 7,631°.
De 'vezels' in deze balk liggen nu niet meer evenwijdig
met de balk-as, maar neigen steeds meer naarmate ze
verder naar buiten liggen. Door het buigend moment
ontstaan spanningen in de balk die, doordat de vezels
Figuur 4. Betekenis snijpunt in relatie tot inwendige dwarskracht in vakwerk
Figuur 5. Uitkragende ligger met verlopende hoogte Figuur 6. Verticale krachten als gevolg
van het buigend moment
Normbesef (7)
CEMENT 6 2024 ?49
? Leonhardt beschrijft dit fenomeen in paragraaf 8.6.2 [1].
Daarbij wordt uitsluitend ingegaan op met beugels
gewapende doorsneden. Wat Leonhardt 50 jaar ge-
leden heeft opgeschreven, vindt nog steeds zijn weer-
slag in de huidige Eurocode. De in dit artikel afgeleide
vergelijking (1) komt in Leonhardt ook terug (als door
E. Mörsch [2] en H. Bay afgeleid [3]):
()
= v vr sin cos
sin
lh
() = + DL V cos sin
FF
= +OL OR DR cos cos
F FF
= BL BR DL cos cos
F FF
( )
= V DR sin
cos
FF
?? ?? = = = ?? ??
?? ??
h h
2
2 2
M yy
_h _h
2 2
2
2
M y y DxDy M DxDy M DxDy Vb dyy b dy
h
I Ihh
= = \fit
in \fit M \fitM DxDy VVVV h
= = \fit
in \fit 3, \b31 0, 268 0
1
V
VV
red = tan M
QQ h
Waarbij ? de som van de hellingen van de buitenzijde
van de ligger is.
? Het berekenen van het dwarskrachtdraagvermogen
van liggers zonder beugels is nog voor een groot ge-
deelte gestoeld op empirisch onderzoek. Er lijkt onvol-
doende onderzoek te zijn gedaan om artikel 6.2.1(2)
van EN 1992-1-1 ook van toepassing te kunnen verkla-
ren voor constructies zonder dwarskrachtwapening.
Het artikel moet wellicht wel worden uitgebreid, omdat
een verlopende hoogte ook blijkt te kunnen leiden tot
een toename van de dwarskracht.
Conclusie
Een verlopende hoogte heeft effect op de grootte van
de dwarskracht in de constructie, ongeacht of uitgegaan
wordt van een vakwerk of een balkvormige constructie.
De dwarskracht blijkt te kunnen afnemen ten opzichte van
de op de ligger uitgeoefende dwarskracht, maar onder
bepaalde voorwaarden ook juist te kunnen toenemen.
De meeste door constructeurs gebruikte software houdt
echter geen rekening met dit fenomeen, waardoor de
constructeur dit zelf zal moeten verwerken.
De vraag kan worden gesteld hoe belangrijk het is om
rekening te houden met dit effect. Belangrijk daarbij is
te beseffen dat voutes veelal juist worden toegepast
om geen dwarskrachtwapening te hoeven toepassen.
Zolang de dwarskracht alleen kleiner wordt, is dat geen
enkel probleem. Het kan wel problematisch worden als
de dwarskracht van teken omkeert en zelfs groter
wordt dan de dwarskracht volgens de oorspronkelijke
dwarskrachtenlijn. Er zijn bij de auteur een paar voor-
beelden bekend waar dit een rol zou kunnen spelen.?
Literatuur
1. Leonhardt, F., & Mönnig, E., Vorlesungen über
Massivbau - Erster Teil - Grundlagen zur Bemessung im
Stahlbetonbau. Stuttgart: Springer Verlag, 1973.
2. Mörsch, E., Die Bemessung im Eisenbetonbau ?
5 Aufl., Stuttgart, Konrad Wittwer, 1950.
3. Bay, H., Wandartige Träger und Bogenscheiben.
Stuttgart, Konrad Wittwer, 1960.
niet evenwijdig aan de zwaartelijn liggen, ook een ver-
ticale component hebben (fig. 6).
De grootte van deze verticale component ten gevolge
van het uitgeoefende moment M volgt uit:
()
= v vr sin cos
sin
lh
() = + DL V cos sin
FF
= +OL OR DR cos cos
F FF
= BL BR DL cos cos
F FF
( )
= V DR sin cos
FF
?? ?? = = = ?? ??
?? ??h h
2
2 2
M yy
_h _h
2 2
2
2
M y y DxDy M DxDy M DxDy Vb dyy b dy h
I Ihh
= = \fit
in \fit M \fitM DxDy VVVV h
= = \fit
in \fit3, \b31 0, 268 0
1
V
VV
red = tan M
QQ h
Waarin DxDy = (h l ? h r) / l - de relatieve hoogtetoename
van de ligger
De grootte van de inwendige dwarskracht in iedere sne -
de, ongeacht de vorm van de doorsnede, volgt dus uit:
()
= v vr sin cos
sin
lh
() = + DL V cos sin
FF
= +OL OR DR cos cos
F FF
= BL BR DL cos cos
F FF
( )
= V DR sin
cos
FF
?? ?? = = = ?? ??
?? ??
h h
2
2 2
M yy
_h _h
2 2
2
2
M y y DxDy M DxDy M DxDy Vb dyy b dy
h
I Ihh
= = \fit
in \fit M \fitM DxDy VVVV h
= = \fit
in \fit 3, \b31 0, 268 0
1
V
VV
red = tan M
QQ h
(1)
Waarin h de hoogte van de beschouwde doorsnede is.
Voor een ligger waarbij de boven- en onderrand een
hoek ? = 7,631° hebben, geldt DxDy = 0,268. Het snij-
punt van de boven- en onderrand van de ligger ligt bij
een hoogte h
r = 1 m op 1 m / 0,268 = 3,731 m rechts van
het balkeinde. Als de uitwendige dwarskracht als het
ware aangrijpt in dit punt geldt voor V
in:
uit
in uit 3, 731 0, 268 0 1
V VV =
=
Eenvoudig is na te gaan dat dit voor iedere doorsnede
in deze uitkragende ligger zal gelden.
Vergelijking (1) is toepasbaar voor elk type doorsnede,
en zelfs op het vakwerk. Nadere bestudering leert:
? Eerder was al getoond dat een groot uitgeoefend
moment in verhouding tot de uitgeoefende dwars-
kracht tot omkering van de dwarskracht kan leiden.
Deze bevinding volgt ook uit vergelijking (1).
? Bij een ligger die lager wordt naar de oplegging toe,
is DxDy negatief. Hierdoor zal de inwendige dwars-
kracht in de ligger toenemen en groter worden dan de
uitwendige dwarskracht.
? Bij een ligger waarbij het moment een tegengesteld
teken heeft zal de inwendige dwarskracht ook groter
worden dan de uitwendige dwarskracht.
Waarom niet voor doorsneden zonder
dwarskrachtwapening?
De vraag kan worden gesteld waarom artikel 6.2.1(2)
niet geldt voor liggers zonder dwarskrachtwapening.
Hier is op dit moment geen eenduidig antwoord op
mogelijk, maar kan wel het volgende worden opge-
merkt:
Rectificatie: verkeerde figuren in vakblad
Helaas is er in de papieren publicatie van dit artikel, in het vakblad, een fout geslopen. Hierdoor zijn de verkeerde figuur 3 en figuur 4 geplaatst. In deze online publicatie staan beide figuren wel juist weergegeven.
Rubriek Normbesef
Dit is het zevende artikel in de Cement-rubriek Normbesef. In deze rubriek kunnen lezers onduidelijkheden in de constructeurspraktijk, bijvoorbeeld in de regelgeving, aankaarten.
Let wel: Hoewel de artikelen worden beoordeeld door experts, betreft het de persoonlijke interpretatie van de auteur. Aan de inhoud kunnen dan ook geen rechten worden ontleend. De artikelen geven ook niet altijd een antwoord of oplossing.
Het doel van de rubriek is de sector te informeren over onduidelijkheden en daarmee een discussie op gang brengen. Dit kan leerzaam zijn, zo meent de redactie van Cement. Uiteraard voor de normcommissie, maar ook voor collega-constructeurs. Het uiteindelijke doel van de rubriek is meer duidelijkheid voor iedereen en in sommige gevallen misschien zelfs betere normen.
Een uitgebreidere toelichting op de rubriek staat in het artikel ‘Nieuwe rubriek over normen: Normbesef’ op Cementonline.
Heb je zelf ook een onderwerp voor deze rubriek, neem dan contact op met Jacques Linssen, j.linssen@aeneas.nl. Publicatie kan eventueel anoniem.
Iedere constructeur kent wel artikel 6.2.1(2) uit NEN-EN 1992-1-1 (EC2), waarin staat aangegeven dat de dwarskrachtweerstand van een element met dwarskrachtwapening gelijk is aan (formule 6.1):
VRd = VRd,s + Vccd + Vtd
Voor elementen met verlopende hoogte wordt deze vergelijking toegelicht met figuur 6.2 uit Eurocode 2 (fig. 1). Feitelijk komt het erop neer dat de voor dwarskracht benodigde hoeveelheid beugels in een ligger met verlopende hoogte mag worden gereduceerd tot:
VRd,s = VRd - Vccd - Vtd

Figuur 1. Dwarskrachtcomponent voor elementen met verlopende hoogte (figuur 6.2 uit EC2)
Doorsneden met dwarskrachtwapening
Om een beter beeld te krijgen van wat er met een ligger met verlopende hoogte gebeurt, wordt een vakwerkanalogie beschouwd. Daarbij wordt uitgegaan van het in figuur 2 weergegeven vakwerk van een aan één zijde ingeklemde ligger die aan het vrije uiteinde wordt belast door een moment M en dwarskracht V. Een positief moment en dwarskracht komen hierbij overeen met de aangegeven richtingen.
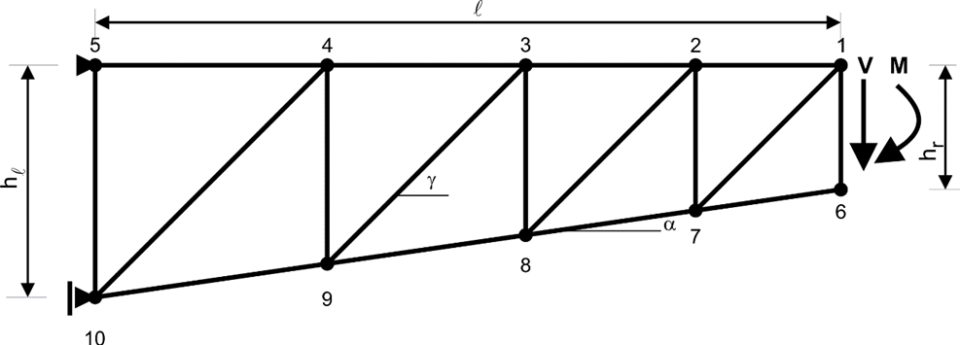
Figuur 2. Vakwerk van ligger met verlopende hoogte
De lengte van de ligger is l, de hoogte links hl en rechts hr. De helling van de onderrandstaaf is α = 15°, en voor de eenvoud die van de diagonalen γ = 45°, en van de bovenrandstaaf β = 0°. De relatie tussen hl en hr volgt dus uit hl = hr + l · tan α.
Als wordt aangenomen dat hr = 1 m, dan geldt voor l = 9,263 m en voor hl = 3,482 m op een heel aantal velden uit te komen.
Voor deze afleiding zijn een aantal goniometrische relaties gebruikt. De horizontaal gemeten lengte van één vak van het vakwerk volgt uit:
met hvr de hoogte van het beschouwde vak aan de rechterzijde. Voor de hoogtetoename geldt
Δh = lv · (tan α + tan β)
De krachten in de verticalen van dit vakwerk worden bepaald voor een dwarskracht V = 10 kN of een moment M = 10 kNm. De resultaten zijn weergegeven in tabel 1.
In het vakwerk gelden de volgende evenwichtsrelaties (fig. 3):
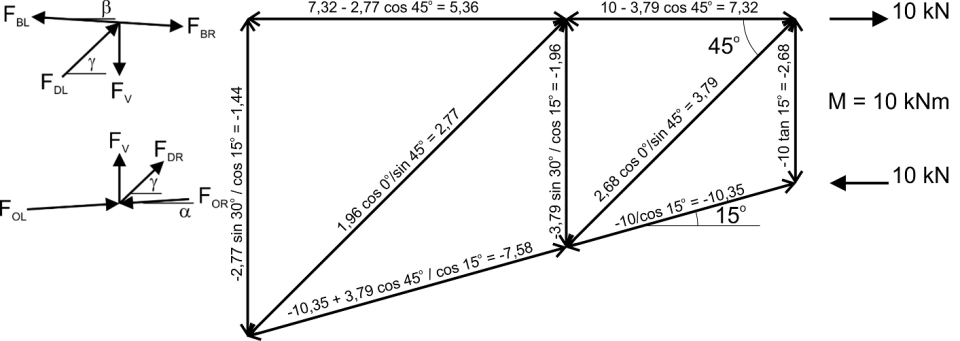
Figuur 3. Evenwichtsrelaties in vakwerk
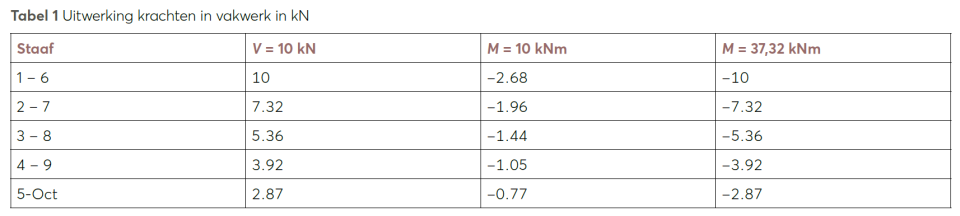
Tabel 1
Het, schijnbaar opvallende, resultaat is dus dat de inwendige dwarskracht in de ligger afneemt terwijl de uitwendige dwarskracht constant blijft. Verder valt op dat door het moment een tegengestelde dwarskracht ontstaat.
Bij het eveneens in tabel 1 weergegeven moment M = 37,32 kNm blijkt de som van de inwendige dwarskracht door de uitgeoefende dwarskracht en moment zelfs nul te worden.
Dit is op zich niet zo vreemd – het snijpunt van de boven- en onderrandstaaf bevindt zich 1 m / tan α = 1 m / tan 15° = 3,73 m rechts van het vakwerk. Een moment M = 37,32 kNm komt dus overeen met een dwarskracht die exact in het snijpunt van de boven- en onderrand aangrijpt, en dus geheel kan worden opgenomen door de normaalkrachten in deze staven.
In figuur 4 wordt weergegeven wat dit betekent. Het moment kan worden gezien als een dwarskracht die met een bepaalde excentriciteit wordt uitgeoefend. Met toenemende excentriciteit neemt de inwendige (niet de uitwendige) dwarskracht af totdat deze nul wordt, als de excentrische dwarskracht samenvalt met het snijpunt van de boven- en onderrand. Wanneer de excentriciteit nog groter wordt, dan zal de inwendige dwarskracht een aan de uitwendige dwarskracht tegengesteld teken krijgen. Bij een moment dat in verhouding groot is ten opzichte van de dwarskracht, kan de inwendige dwarskracht niet alleen van teken omslaan, maar in absolute zin zelfs groter worden dan de uitwendige dwarskracht.
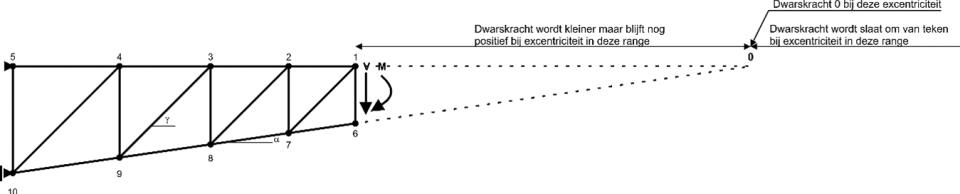
Figuur 4. Betekenis snijpunt in relatie tot inwendige dwarskracht in vakwerk
Wanneer in plaats van α = 15° wordt aangehouden α = 0° en β = 15°, verandert wel de geometrie en krachtswerking in het vakwerk, maar bij een moment M = 37,32 kNm blijft de inwendige dwarskracht nog steeds gelijk aan nul!
Lineair elastische doorsneden
Nu kan de vraag worden gesteld hoe het dan zit met een nog volledig elastische (ongescheurde) ligger. Hiertoe wordt uitgegaan van een uitkragende ligger met constante breedte en verlopende hoogte (fig. 5). Om de afleiding wat eenvoudiger te houden krijgen boven- en onderrand dezelfde helling zodat geldt tan α + tan β = tan 15° => α = β = 7,631°.
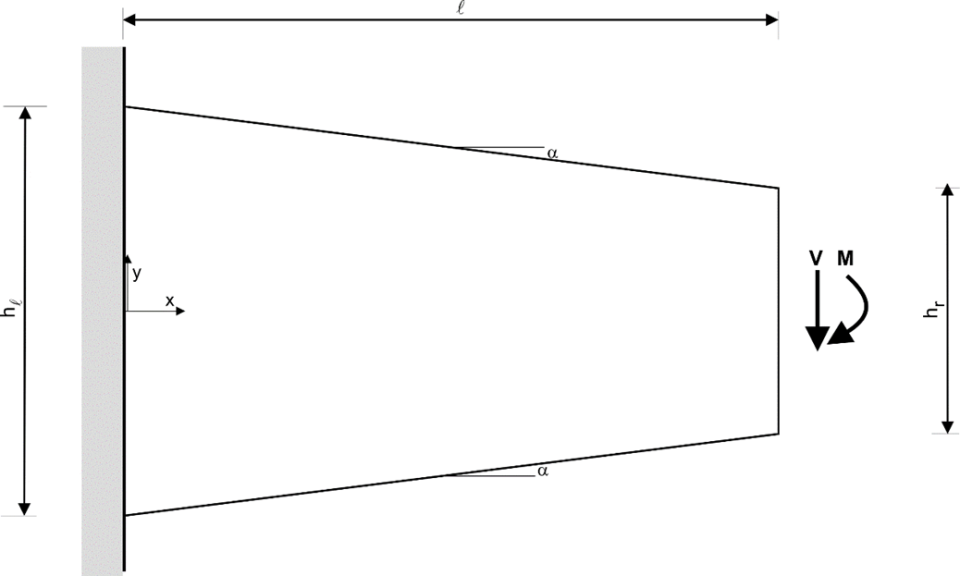
Figuur 5. Uitkragende ligger met verlopende hoogte
De ‘vezels’ in deze balk liggen nu niet meer evenwijdig met de balk-as, maar neigen steeds meer naarmate ze verder naar buiten liggen. Door het buigend moment ontstaan spanningen in de balk die, doordat de vezels niet evenwijdig aan de zwaartelijn liggen, ook een verticale component hebben (fig. 6).
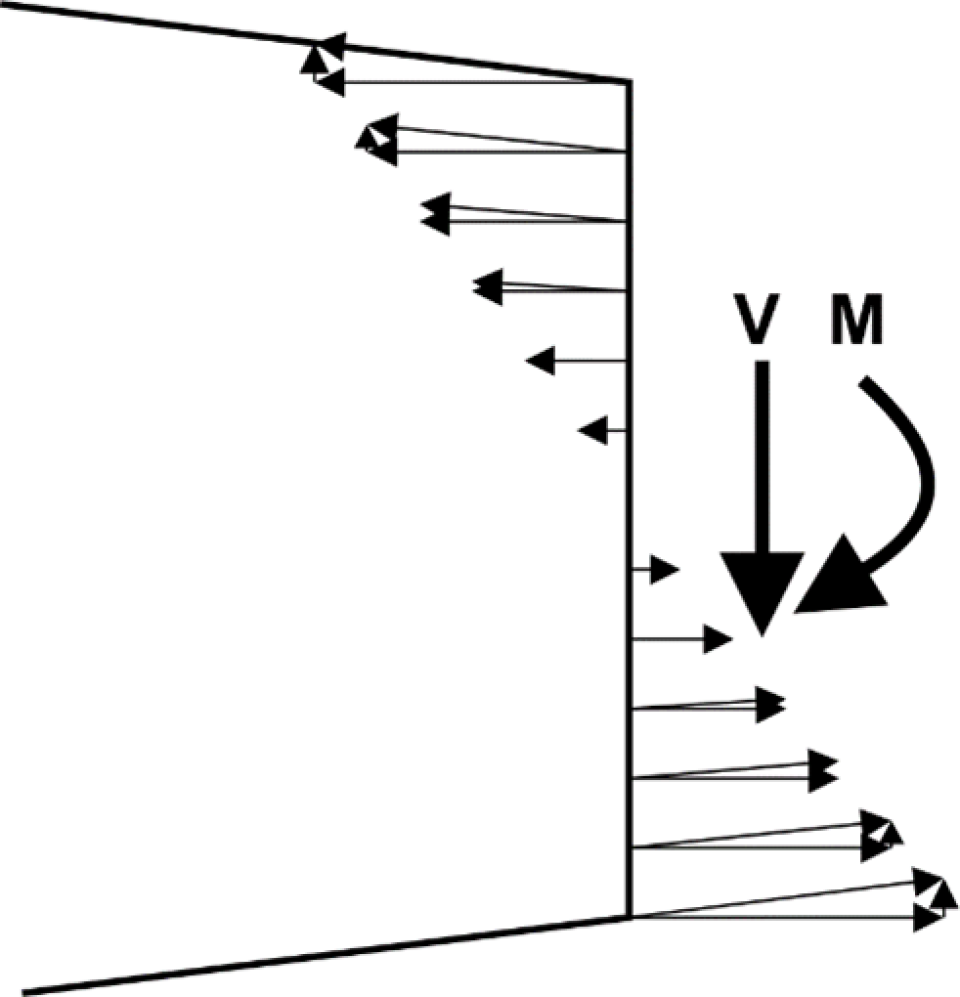
Figuur 6. Verticale krachten als gevolg van het buigend moment
De grootte van deze verticale component ten gevolge van het uitgeoefende moment M volgt uit:
Waarin DxDy = (hl – hr) / l - de relatieve hoogtetoename van de ligger
De grootte van de inwendige dwarskracht in iedere snede, ongeacht de vorm van de doorsnede, volgt dus uit:
Waarin h de hoogte van de beschouwde doorsnede is.
Voor een ligger waarbij de boven- en onderrand een hoek α = 7,631° hebben, geldt DxDy = 0,268. Het snijpunt van de boven- en onderrand van de ligger ligt bij een hoogte hr = 1 m op 1 m / 0,268 = 3,731 m rechts van het balkeinde. Als de uitwendige dwarskracht als het ware aangrijpt in dit punt geldt voor Vin:
Eenvoudig is na te gaan dat dit voor iedere doorsnede in deze uitkragende ligger zal gelden.
Vergelijking (1) is toepasbaar voor elk type doorsnede, en zelfs op het vakwerk. Nadere bestudering leert:
- Eerder was al getoond dat een groot uitgeoefend moment in verhouding tot de uitgeoefende dwarskracht tot omkering van de dwarskracht kan leiden. Deze bevinding volgt ook uit vergelijking (1).
- Bij een ligger die lager wordt naar de oplegging toe, is DxDy negatief. Hierdoor zal de inwendige dwarskracht in de ligger toenemen en groter worden dan de uitwendige dwarskracht.
- Bij een ligger waarbij het moment een tegengesteld teken heeft zal de inwendige dwarskracht ook groter worden dan de uitwendige dwarskracht.
Waarom niet voor doorsneden zonder dwarskrachtwapening?
De vraag kan worden gesteld waarom artikel 6.2.1(2) niet geldt voor liggers zonder dwarskrachtwapening. Hier is op dit moment geen eenduidig antwoord op mogelijk, maar kan wel het volgende worden opgemerkt:
- Leonhardt beschrijft dit fenomeen in paragraaf 8.6.2 [1]. Daarbij wordt uitsluitend ingegaan op met beugels gewapende doorsneden. Wat Leonhardt 50 jaar geleden heeft opgeschreven, vindt nog steeds zijn weerslag in de huidige Eurocode. De in dit artikel afgeleide vergelijking (1) komt in Leonhardt ook terug (als door E. Mörsch [2] en H. Bay afgeleid [3]):
Waarbij φ de som van de hellingen van de buitenzijde van de ligger is.
- Het berekenen van het dwarskrachtdraagvermogen van liggers zonder beugels is nog voor een groot gedeelte gestoeld op empirisch onderzoek. Er lijkt onvoldoende onderzoek te zijn gedaan om artikel 6.2.1(2) van EN 1992-1-1 ook van toepassing te kunnen verklaren voor constructies zonder dwarskrachtwapening. Het artikel moet wellicht wel worden uitgebreid, omdat een verlopende hoogte ook blijkt te kunnen leiden tot een toename van de dwarskracht.
Conclusie
Een verlopende hoogte heeft effect op de grootte van de dwarskracht in de constructie, ongeacht of uitgegaan wordt van een vakwerk of een balkvormige constructie. De dwarskracht blijkt te kunnen afnemen ten opzichte van de op de ligger uitgeoefende dwarskracht, maar onder bepaalde voorwaarden ook juist te kunnen toenemen. De meeste door constructeurs gebruikte software houdt echter geen rekening met dit fenomeen, waardoor de constructeur dit zelf zal moeten verwerken.
De vraag kan worden gesteld hoe belangrijk het is om rekening te houden met dit effect. Belangrijk daarbij is te beseffen dat voutes veelal juist worden toegepast om geen dwarskrachtwapening te hoeven toepassen. Zolang de dwarskracht alleen kleiner wordt, is dat geen enkel probleem. Het kan wel problematisch worden als de dwarskracht van teken omkeert en zelfs groter wordt dan de dwarskracht volgens de oorspronkelijke dwarskrachtenlijn. Er zijn bij de auteur een paar voorbeelden bekend waar dit een rol zou kunnen spelen.
Literatuur
- Leonhardt, F., & Mönnig, E., Vorlesungen über Massivbau - Erster Teil - Grundlagen zur Bemessung im Stahlbetonbau. Stuttgart: Springer Verlag, 1973.
- Mörsch, E., Die Bemessung im Eisenbetonbau – 5. Aufl., Stuttgart, Konrad Wittwer, 1950.
- Bay, H., Wandartige Träger und Bogenscheiben. Stuttgart, Konrad Wittwer, 1960.
Reacties