Nieuwe kleding, nieuwe laptop, nieuwe fiets? Het wordt steeds gewoner om online te shoppen. Maar wat heeft dit eigenlijk voor gevolgen voor de wereld daarachter? Bijvoorbeeld voor de enorme magazijnen die verspreid over het land als paddenstoelen uit de grond schieten. Voor de berekening van dit soort gebouwen is de bedrijfsvloer een belangrijk onderdeel, want de stellingen worden hierop geplaatst en alle interne transport vindt over de vloer plaats. Hoe bereken je zo'n vloer nou eigenlijk, of in een andere rol, hoe controleer je die berekening?
48
Puntlasten op
vloeren vaak
onderschat
Vergelijking Q-last en puntlasten op magazijnvloeren
Puntlasten op vloer vaak onderschat 8 2017
49
Magazijnvloeren worden vaak ontworpen op basis van een
Q-last, een gelijkmatig verdeelde belasting. Dat komt echter
niet overeen met de werkelijke belasting, namelijk stellingen.
Een gelijkmatig verdeelde belasting kan bestaan uit bulkgoe-
deren, of palletlasten direct op de vloer geplaatst. Stellingen
vormen echter een volledig ander belastingsmechanisme. Zo
leidt een indeling met gangpaden en aan beide zijden een
stelling ertoe dat twee stellingpoten rug-aan-rug en dus naast
elkaar op de vloer staan.
Funderingspalen
Als de vloer op palen is gefundeerd, moet de krachtsafdracht
naar die palen kritisch worden beoordeeld. Het paalstramien
wordt op basis van de Q-last gekozen. Maar de draagkracht
van de paal moet wel worden getoetst op de eerdergenoemde
dubbele puntlast, inclusief veiligheid. Want die dubbele puntlast
moet volledig door één paal kunnen worden opgenomen. Bij
een dubbele puntlast van bijvoorbeeld 2 × 95 kN (een gebrui-
kelijke waarde in magazijnen) in gevolgklasse CC1 betekent dit
dat het paaldraagvermogen in ieder geval hoger moet zijn dan
(2 × 95) × 1,35 = 257 kN. Hier is nog geen belasting van pallets
of heftrucks op de vloer in meegenomen. Dat maakt een paal-
diameter van 180 mm al zo goed als onmogelijk.
Vloeren
Ook de vloeren moeten worden getoetst op de dubbele punt-
last. Uit ervaring blijkt dat met name een dunne vloer op een
klein paalstramien kritisch is. Als de in de grond gevormde
palen Ø180 mm op basis van een Q-last van 50 kN/m
2 op een
raster van 1,9 m
2 worden geplaatst, moet dit veld worden
getoetst op de optredende puntlast, en niet alleen op de Q-last.
Bij de toets van de puntlast moet niet alleen het steunpunts-
moment worden getoetst, maar zeker ook het veldmoment,
omdat dat vaak kritisch is of zelfs wordt overschreden. Dat
1
Niels Punt, Lex van der Meer
ABT bv
1 Voor de berekening
van magazijnen is de
bedrijfsvloer een
belangrijk onderdeel
Nieuwe kleding, nieuwe laptop, nieuwe fiets? Het wordt steeds gewoner
om online te shoppen. Maar wat heeft dit eigenlijk voor gevolgen voor de
wereld daarachter? Bijvoorbeeld voor de enorme magazijnen die verspreid
over het land als paddenstoelen uit de grond schieten. Voor de berekening
van dit soort gebouwen is de bedrijfsvloer een belangrijk onderdeel, want
de stellingen worden hierop geplaatst en alle interne transport vindt over
de vloer plaats. Hoe bereken je zo'n vloer nou eigenlijk, of in een andere rol,
hoe controleer je die berekening?
Puntlasten op vloer vaak onderschat 8 2017
50
2 Configuratie van twee jukken rug-aan-rug
3 EEM-model van de vloer met palen (rood) en puntlasten (geel)
45 kN/m 2. Dit is dus een fractie lager dan de veranderlijke
vloerbelasting. Op basis van deze beschouwing is het belastings-
geval met de puntlasten niet maatgevend. Uit het volgende zal
blijken dat het tegendeel waar is.
EEM-berekening
Om de daadwerkelijke invloed van de puntlasten te toetsen,
kan de werkelijkheid het best worden benaderd door een niet-
lineaire EEM-berekening op te stellen. Hierin worden de para-
meters van de vloer, de wapening, de palen en de puntlasten
met hun eigenschappen gemodelleerd. Natuurlijk is de capaci-
teit van de vloer en wapening daarbij belangrijk, maar het
gekozen paalstramien speelt ook een rol. Dat bepaalt namelijk
hoe groot het veld is waarover de kracht kan worden verspreid.
Er geldt dus dat bij een kleiner veld het vloeroppervlak waarover
de lasten kunnen worden verdeeld kleiner is en dat een kleiner
paalstramien dus niet per definitie gunstiger is.
In een EEM-model wordt een klein segment uit de vloer gemo-
delleerd waarbij aan de randen van het segment dusdanige
eigenschappen (symmetrierandvoorwaarden) worden toegekend
dat dit precies gelijk is aan een doorgaande vloer. Aan de
onderzijde van de vloer worden de palen gemodelleerd waarna
de berekening kan worden uitgevoerd. Het EEM-model is
opgebouwd uit kwadratische volume-elementen. Over de dikte
van de vloer zijn zes elementen toegepast. De maximale
elementgrootte in het vlak van de vloer is 200 mm. Ter plekke
van de palen en de puntlasten is het elementennet verfijnd.
Een voorbeeld van een EEM-model van een vloer met punt-
lastenstramien is te zien in figuur 3. Het grijze grid is de vloer,
met daarop in rood aangegeven de positie van de palen en in
het geel de puntlasten uit stellingen. De gele blokken die het
dichtst bij elkaar staan, symboliseren de stellingpoten die
rug-aan-rug staan, de overige poten grenzen aan een gangpad.
Dit is de meest voorkomende belasting, maar de puntlasten
kunnen ook worden gecombineerd met een palletlast onder
de stellingen en een heftruck in het gangpad, of elke andere
gewenste belasting.
komt de duurzaamheid niet ten goede in het geval van scheur
-
vorming, maar het kan ook tot bezwijken leiden. In het geval
van een stellingenmagazijn kan dat persoonlijk letsel tot gevolg
hebben. Dus niet alleen de gemaakte sommetjes moeten goed
worden gecontroleerd, er moet ook worden bedacht of alle
mogelijke risico's zijn getoetst.
Praktijkvoorbeeld
Om de invloed van puntlasten te onderbouwen, volgt een
praktijkvoorbeeld: de veranderlijke vloerbelasting bedraagt
Q = 50 kN/m
2 en puntlasten zijn 2 × 95 kN rug-aan-rug. Deze
puntlasten kunnen als een last van 190 kN worden beschouwd
omdat ze op slechts een afstand van 300 mm staan. Het vloer-
stramien is 2,05 × 2,05 m
2 (fig. 2).
Q-last
Het uitsmeren van de puntlasten over twee stramienen van
de vloer leidt tot een equivalente Q-last van 4 × 95 / 2 / 2,05
2 =
2
3
Puntlasten op vloer vaak onderschat 8 2017
51
4
Staalvezelbeton onder trek (overzicht)
5 Staalvezelbeton onder trek (detail)
6 Staalvezelbeton onder druk 7
Wapeningsstaal
8 Lastzakkingsdiagram van de vloer
De volgende bezwijkcriteria worden doorgaans gehanteerd:
? De rek van beton onder druk is groter dan 3,5?.
? De rek van staalvezelbeton onder trek is groter dan 2,5%.
? De rek van wapening onder trek is groter dan 4,5%.
? De berekening heeft geen acceptabele convergentie meer.
Het scheuren van beton en het vloeien van wapening verlagen
de stijfheid van de vloer. Dit wordt inzichtelijk gemaakt met
behulp van een lastzakkingsdiagram, dat volgt uit de EEM-
berekening (fig. 8). In dit diagram is de maximale doorbuiging Reklimieten
In de berekening zijn de volgende uitgangspunten gehanteerd:
- betonsterkteklasse C35/45
- staalvezels 35 kg/m
3
- lengte staalvezels 50 mm, met eindverankering
- f
eqm1 3,7 MPa
- f
eqm4 3,5 MPa
- dekking betonstaal 40 mm
- bovennet Ø7-100
- bijlegwapening boven Ø8-150
- verticale paalstijfheid 30 MN/m
Het spanning-rekdiagram uit CUR-Aanbeveling 111 is
gehanteerd. De diagrammen uit dit voorbeeld zijn weergegeven
in figuur 4 t/m 7. De belasting wordt stapsgewijs steeds verder
opgevoerd tot aan het punt van bezwijken van de constructie.
Omdat niet-lineair materiaalgedrag wordt mee-genomen in de
berekening, kan bezwijken niet op basis van spanningen
worden vastgesteld. De spanning kan immers
de opgegeven sterkte niet overschrijden. Reklimieten kunnen
wel worden gebruikt om bezwijken te definiëren. Daarnaast
is het belangrijk te controleren of de niet-lineaire berekening
voldoende nauwkeurig is (acceptabele convergentie van het
iteratieproces).
? rek [?]
geconvergeerd
niet geconvergeerd
120
100
80
60
40
200
? maximale doorbuiging [mm]
0 20 40 \
60 80
?
representatieve puntlast [kN]
0 5 10 1\
5 20 25 30 ? trekspanning [MPa]
UGT; 25.00; 1.04
UGT; 0.20; 1.33
3
2,5 2
1,5 1
0,5 0
3
2,5 2
1,5 1
0,5 0
? rek [?]
? trekspanning [MPa]
UGT; 0.12; 2.56
UGT; 0.20; 1.33
0 0,2 0,4 \
0,6 0,8 1\
UGT; 0.22; 435
? spanning [MPa]
500
450
400
350
300
250
200
150
100
500
? rek [%] UGT; 4.50; 466
0 1 2 \
3 4 5 ? rek [?]
spanning [MPa] ?
UGT; -1.75; 23.33
-10 -8 -6 \
-4 -2 0
4 5
6 7
8
Puntlasten op vloer vaak onderschat 8 2017
52
9 Maximale rek onder druk beton; maximale waarde is 3,2?
10 Maximale rek in de trekzone maximale waarde is 2,3%
11 Spanning in de bovenwapening
12 Rek in de bovenwapening
van de vloer weergegeven ten opzichte van de representatieve
waarde van één puntlast. Het gestippelde traject betreft niet-
geconvergeerde belastingsstappen. Op basis van dit diagram is
de maximaal opneembare puntlast uit een stelling 95 kN per
stellingpoot. Dit betreft de laatste geconvergeerde belastings-
stap. Na controle van de reklimieten blijkt dat deze bij een
puntlast van 95 kN worden overschreden. Op basis van de
reklimieten is de maximaal opneembare puntlast uit een
stelling gelijk aan 91,5 kN. De reklimieten worden in de
EEM-berekening gecontroleerd bij de rekenwaarde van deze
puntlast (1,35 × 91,5 = 123,5 kN). Figuur 9 laat zien dat de
maximale rek in het beton in de drukzone in het midden van
de vloer een waarde bereikt van 3,2?. De drukzone voldoet
hiermee nog net.
Figuur 10 toont de onderzijde van de vloer. Bij dezelfde belas-
tingsstap (representatieve puntlast 91,5 kN) is de rek in de
trekzone van het staalvezelbeton maximaal 2,3%. De trekzone
voldoet hiermee ook nog net.
Figuur 11 en 12 tonen de spanning en de rek in de bovenwape-
ning. Hoewel de bovenwapening zich vlakbij de neutrale lijn
bevindt, vloeit deze lokaal. De maximale rek in de bovenwape-
ning is 0,32%, inderdaad groter dan 435 / 200.000 = 0,22%,
de rek waarbij de wapening gaat vloeien.
Conclusie
Uit het lastzakkingsdiagram volgde een representatieve
opneembare puntlast van 91,5 kN. De rekken van het staalvezel-
beton en de wapening bevestigen dat dit een situatie dicht bij
bezwijken betreft. De puntlast van 95 kN is dus net niet
opneembaar; de bijbehorende unity check is 95 / 91,5 = 1,04.
Door de werkelijke belastingen op de vloer te plaatsen en de
vloer te modelleren met zo realistisch mogelijke eigenschappen,
wordt de berekening waarheidsgetrouw. De EEM-berekening
laat zien dat de puntlasten net niet opneembaar zijn door de
gemodelleerde vloer, terwijl op basis van de equivalente Q-last
de conclusie werd getrokken dat de puntlasten niet maatgevend
zijn. In de praktijk komt het ook regelmatig voor dat de daad-
werkelijke toetsing van de puntlasten achterwege blijft.
Aangezien fulfilment (het hele logistieke verhaal van magazijn
tot klant) steeds meer centraliseert en distributiecentra groter
en hoger worden, neemt de vraag naar specifiek ontwerpen en
een goede beschouwing van de krachten toe.
Daarbij worden er (naast een specifieke puntlast) ook steeds
meer eisen aan de vervorming van een vloer gesteld. Hierdoor
wordt hoogwaardige kennis van alle aspecten van bedrijfs-
vloeren steeds belangrijker ? en hoogwaardig rekenen dus
noodzakelijk.
?
Puntlasten op vloer vaak onderschat 8 2017

1. Voor de berekening van dit soort gebouwen is de bedrijfsvloer een belangrijk onderdeel
Magazijnvloeren worden vaak ontworpen op basis van een Q-last, een gelijkmatig verdeelde belasting. Dat komt echter niet overeen met de werkelijke belasting, namelijk stellingen. Een gelijkmatig verdeelde belasting kan bestaan uit bulkgoederen, of palletlasten direct op de vloer geplaatst. Stellingen vormen echter een volledig ander belastingsmechanisme. Zo leidt een indeling met gangpaden en aan beide zijden een stelling ertoe dat twee stellingpoten rug-aan-rug en dus naast elkaar op de vloer staan.
Funderingspalen
Als de vloer op palen is gefundeerd, moet de krachtsafdracht naar die palen kritisch worden beoordeeld. Het paalstramien wordt op basis van de Q-last gekozen. Maar de draagkracht van de paal moet wel worden getoetst op de eerdergenoemde dubbele puntlast, inclusief veiligheid. Want die dubbele puntlast moet volledig door één paal kunnen worden opgenomen. Bij een dubbele puntlast van bijvoorbeeld 2 × 95 kN (een gebruikelijke waarde in magazijnen) in gevolgklasse CC1 betekent dit dat het paaldraagvermogen in ieder geval hoger moet zijn dan (2 × 95) × 1,35 = 257 kN. Hier is nog geen belasting van pallets of heftrucks op de vloer in meegenomen. Dat maakt een paaldiameter van 180 mm al zo goed als onmogelijk.
Vloeren
Ook de vloeren moeten worden getoetst op de dubbele puntlast. Uit ervaring blijkt dat met name een dunne vloer op een klein paalstramien kritisch is. Als de in de grond gevormde palen Ø180 mm op basis van een Q-last van 50 kN/m2 op een raster van 1,9 m2 worden geplaatst, moet dit veld worden getoetst op de optredende puntlast, en niet alleen op de Q-last. Bij de toets van de puntlast moet niet alleen het steunpuntsmoment worden getoetst, maar zeker ook het veldmoment, omdat dat vaak kritisch is of zelfs wordt overschreden. Dat komt de duurzaamheid niet ten goede in het geval van scheurvorming, maar het kan ook tot bezwijken leiden. In het geval van een stellingenmagazijn kan dat persoonlijk letsel tot gevolg hebben. Dus niet alleen de gemaakte sommetjes moeten goed worden gecontroleerd, er moet ook worden bedacht of alle mogelijke risico’s zijn getoetst.
Praktijkvoorbeeld
Om de invloed van puntlasten te onderbouwen, volgt een praktijkvoorbeeld: de veranderlijke vloerbelasting bedraagt Q = 50 kN/m2 en puntlasten zijn 2 × 95 kN rug-aan-rug. Deze puntlasten kunnen als een last van 190 kN worden beschouwd omdat ze op slechts een afstand van 300 mm staan. Het vloerstramien is 2,05 × 2,05 m2 (fig. 2).
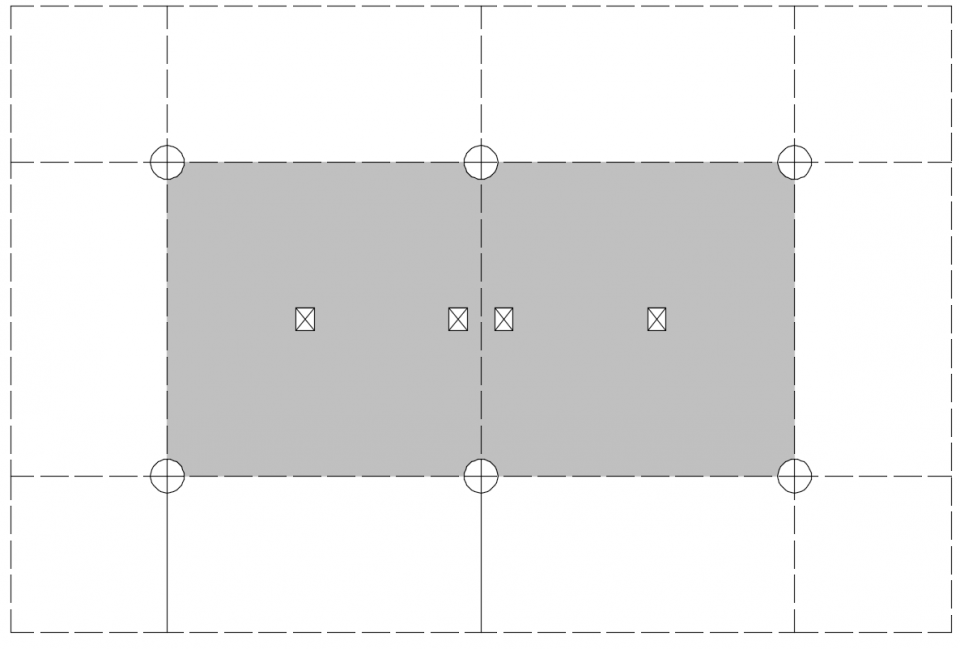
2. Configuratie van twee jukken rug-aan-rug
Q-last
Het uitsmeren van de puntlasten over twee stramienen van de vloer leidt tot een equivalente Q-last van 4 × 95 / 2 / 2,052 = 45 kN/m2. Dit is dus een fractie lager dan de veranderlijke vloerbelasting. Op basis van deze beschouwing is het belastingsgeval met de puntlasten niet maatgevend. Uit het volgende zal blijken dat het tegendeel waar is.
EEM-berekening
Om de daadwerkelijke invloed van de puntlasten te toetsen, kan de werkelijkheid het best worden benaderd door een niet-lineaire EEM-berekening op te stellen. Hierin worden de parameters van de vloer, de wapening, de palen en de puntlasten met hun eigenschappen gemodelleerd. Natuurlijk is de capaciteit van de vloer en wapening daarbij belangrijk, maar het gekozen paalstramien speelt ook een rol. Dat bepaalt namelijk hoe groot het veld is waarover de kracht kan worden verspreid. Er geldt dus dat bij een kleiner veld het vloeroppervlak waarover de lasten kunnen worden verdeeld kleiner is en dat een kleiner paalstramien dus niet per definitie gunstiger is.
In een EEM-model wordt een klein segment uit de vloer gemodelleerd waarbij aan de randen van het segment dusdanige eigenschappen (symmetrierandvoorwaarden) worden toegekend dat dit precies gelijk is aan een doorgaande vloer. Aan de onderzijde van de vloer worden de palen gemodelleerd waarna de berekening kan worden uitgevoerd. Het EEM-model is opgebouwd uit kwadratische volume-elementen. Over de dikte van de vloer zijn zes elementen toegepast. De maximale elementgrootte in het vlak van de vloer is 200 mm. Ter plekke van de palen en de puntlasten is het elementennet verfijnd.
Een voorbeeld van een EEM-model van een vloer met puntlastenstramien is te zien in figuur 3. Het grijze grid is de vloer, met daarop in rood aangegeven de positie van de palen en in het geel de puntlasten uit stellingen. De gele blokken die het dichtst bij elkaar staan, symboliseren de stellingpoten die rug-aan-rug staan, de overige poten grenzen aan een gangpad. Dit is de meest voorkomende belasting, maar de puntlasten kunnen ook worden gecombineerd met een palletlast onder de stellingen en een heftruck in het gangpad, of elke andere gewenste belasting.
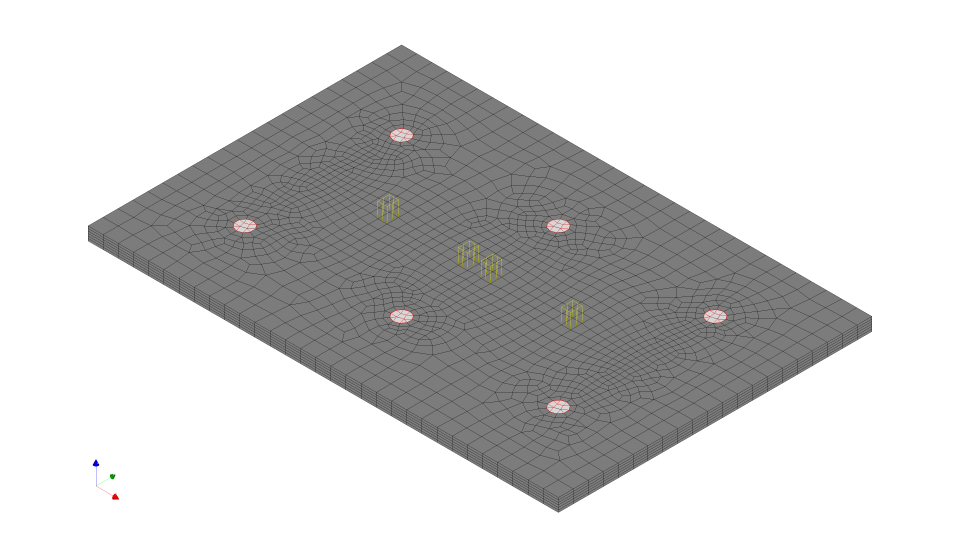
3. EEM-model van de vloer met palen (rood) en puntlasten (geel)
Reklimieten
In de berekening zijn de volgende uitgangspunten gehanteerd:
- betonsterkteklasse: C35/45
- staalvezels: 35 kg/m3
- lengte staalvezels: 50 mm, met eindverankering
- feqm1: 3,7 MPa
- feqm4: 3,5 MPa
- dekking betonstaal: 40 mm
- bovennet: Ø7-100
- bijlegwapening boven: Ø8-150
- verticale paalstijfheid: 30 MN/m
Het spanning-rekdiagram uit CUR-Aanbeveling 111 is gehanteerd. De diagrammen uit dit voorbeeld zijn weergegeven in figuur 4 t/m 7. De belasting wordt stapsgewijs steeds verder opgevoerd tot aan het punt van bezwijken van de constructie. Omdat niet-lineair materiaalgedrag wordt meegenomen in de berekening, kan bezwijken niet op basis van spanningen worden vastgesteld. De spanning kan immers de opgegeven sterkte niet overschrijden. Reklimieten kunnen wel worden gebruikt om bezwijken te definiëren. Daarnaast is het belangrijk te controleren of de niet-lineaire berekening voldoende nauwkeurig is (acceptabele convergentie van het iteratieproces).
De volgende bezwijkcriteria worden doorgaans gehanteerd:
- De rek van beton onder druk is groter dan 3,5‰.
- De rek van staalvezelbeton onder trek is groter dan 2,5%.
- De rek van wapening onder trek is groter dan 4,5%.
- De berekening heeft geen acceptabele convergentie meer.
4. Staalvezelbeton onder trek (overzicht)
5. Staalvezelbeton onder trek (detail)
6. Staalvezelbeton onder druk
Het scheuren van beton en het vloeien van wapening verlagen de stijfheid van de vloer. Dit wordt inzichtelijk gemaakt met behulp van een lastzakkingsdiagram, dat volgt uit de EEM-berekening (fig. 8). In dit diagram is de maximale doorbuiging van de vloer weergegeven ten opzichte van de representatieve waarde van één puntlast. Het gestippelde traject betreft niet-geconvergeerde belastingsstappen. Op basis van dit diagram is de maximaal opneembare puntlast uit een stelling 95 kN per stellingpoot. Dit betreft de laatste geconvergeerde belastingsstap. Na controle van de reklimieten blijkt dat deze bij een puntlast van 95 kN worden overschreden. Op basis van de reklimieten is de maximaal opneembare puntlast uit een stelling gelijk aan 91,5 kN. De reklimieten worden in de EEM-berekening gecontroleerd bij de rekenwaarde van deze puntlast (1,35 × 91,5 = 123,5 kN). Figuur 9 laat zien dat de maximale rek in het beton in de drukzone in het midden van de vloer een waarde bereikt van 3,2‰. De drukzone voldoet hiermee nog net.
Figuur 10 toont de onderzijde van de vloer. Bij dezelfde belastingsstap (representatieve puntlast 91,5 kN) is de rek in de trekzone van het staalvezelbeton maximaal 2,3%. De trekzone voldoet hiermee ook nog net.
Figuur 11 en 12 tonen de spanning en de rek in de bovenwapening. Hoewel de bovenwapening zich vlakbij de neutrale lijn bevindt, vloeit deze lokaal. De maximale rek in de bovenwapening is 0,32%, inderdaad groter dan 435 / 200.000 = 0,22%, de rek waarbij de wapening gaat vloeien.
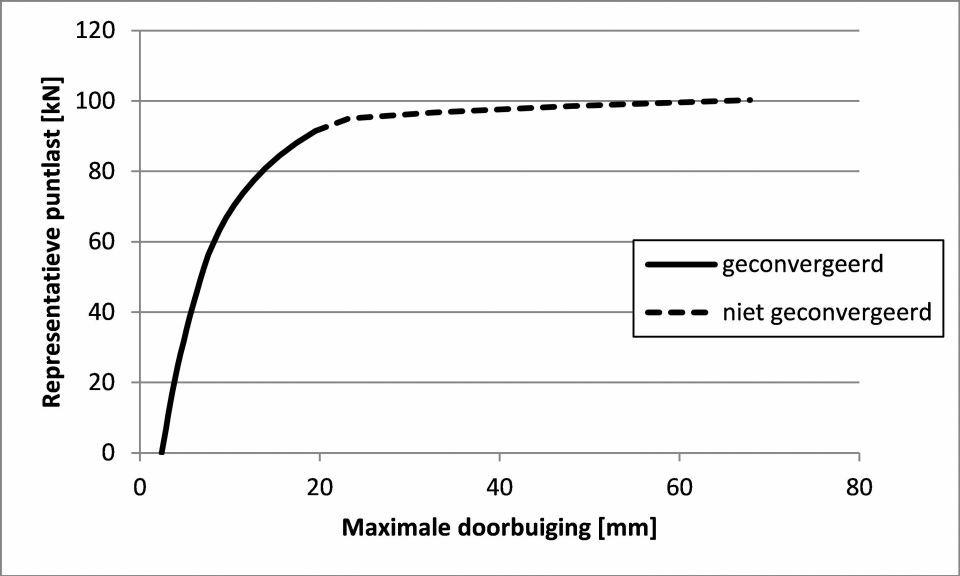
8. Lastzakkingsdiagram van de vloer
Conclusie
Uit het lastzakkingsdiagram volgde een representatieve opneembare puntlast van 91,5 kN. De rekken van het staalvezelbeton en de wapening bevestigen dat dit een situatie dicht bij bezwijken betreft. De puntlast van 95 kN is dus net niet opneembaar; de bijbehorende unity check is 95 / 91,5 = 1,04.
Door de werkelijke belastingen op de vloer te plaatsen en de vloer te modelleren met zo realistisch mogelijke eigenschappen, wordt de berekening waarheidsgetrouw. De EEM-berekening laat zien dat de puntlasten net niet opneembaar zijn door de gemodelleerde vloer, terwijl op basis van de equivalente Q-last de conclusie werd getrokken dat de puntlasten niet maatgevend zijn. In de praktijk komt het ook regelmatig voor dat de daadwerkelijke toetsing van de puntlasten achterwege blijft.
Aangezien fulfilment (het hele logistieke verhaal van magazijn tot klant) steeds meer centraliseert en distributiecentra groter en hoger worden, neemt de vraag naar specifiek ontwerpen en een goede beschouwing van de krachten toe.
Daarbij worden er (naast een specifieke puntlast) ook steeds meer eisen aan de vervorming van een vloer gesteld. Hierdoor wordt hoogwaardige kennis van alle aspecten van bedrijfsvloeren steeds belangrijker – en hoogwaardig rekenen dus noodzakelijk.
9. Maximale rek onder druk beton; maximale waarde is 3,2‰
10. Maximale rek in de trekzone maximale waarde is 2,3%
11. Spanning in de bovenwapening
12. Rek in de bovenwapening
Reacties
Jantine van Steenbergen - DIANA FEA B.V. 01 december 2017 11:54
Goed dat jullie hier ook aandacht aan schenken. Nederland distributie land is veilig maar moet ook in de toekomst veilig blijven. De verhoging van de stellinglasten is inderdaad echt een zichtbare trend. Ab van den Bos - DIANA FEA BV