EEM-software biedt de functionaliteit om op basis van lineair-elastische schijfkrachten en plaatmomenten wapening te bepalen. Maar de optie ontbreekt in de regel voor wapenen op dwarskracht. Dit artikel wil a EEM-software biedt de functionaliteit om op basis van de lineair-elastische resultaten wapening te bepalen. Die aanpak heeft een goede basis voor schijfkrachten en een minder betrouwbare voor plaat- en schaalmomenten. Maar de optie ontbreekt in de regel voor dwarskrachten. Dit artikel wil attenderen op beschikbare kennis en vooral hoe die zich laat implementeren. Demonstraties gebeuren met het programma XFEM4U van Struct4U met een hybride plaatelement.
Van dit artikel is een korte versie verschenen in Cement 2021/8. Deze korte versie is ook online te raadplegen: ‘Wapenen van schijven en platen [kort]’.
Dat EEM-software wapening kan berekenen weet elke constructeur die ermee vertrouwd is. Maar wie zou vragen naar de achterliggende gedachte van zo’n berekening kan teleurgesteld uitkomen. Je krijgt er vaak geen antwoord op. Hij of zij vindt het wel goed. In Cement 2014/3 hebben Braam en Blaauwendraad al eens uitgelegd hoe dat toegaat op basis van lineair-elastische spanningen [1] na een vroege aanzet in 1995 van Lourenço en Blaauwendraad [2]. Maar of het werkelijk geland is? Wellicht was de presentatie nog niet praktisch genoeg of te kort door de bocht. Het is te vrezen dat het betoog voor de gemiddelde lezer een formulebrij is gebleven. In dit artikel presenteren de auteurs de stof op een alternatieve wijze door een (nog) groter beroep te doen op inzicht en onder gebruikmaking van de vertrouwde werkwijze van de vakwerkanalogie. De lezer is dus gewaarschuwd. Er wordt niet zozeer nieuwe kennis ontwikkeld, maar dit artikel beoogt bestaande kennis die niet of nauwelijks gebruikt (begrepen?) wordt beter te ontsluiten. Vergeleken met de genoemde eerdere Cement-publicaties wordt ook meer aandacht geschonken aan hoe een en ander zijn weg kan vinden in programmatuur.
De bestaande kennis voor schijfwapening is het meest vertrouwd. Toch zal ook die wapening op de alternatieve manier worden besproken omdat dezelfde aanpak geschikt is voor het berekenen van plaatwapening. Voor de momentwapening is dat misschien nog niet zo belangrijk, maar vooral als in platen zowel op moment als op dwarskracht moet worden gewapend is de alternatieve presentatie van de schijfwapening handig te gebruiken. Constructeurs zullen dwarskrachtwapening in platen zo veel mogelijk vermijden. Als regel is het goedkoper om een grotere plaatdikte te kiezen of de betonsterkteklasse te verhogen, maar dat is niet altijd de beste oplossing. Het toegankelijk maken van het dwarskrachtprobleem en de uitleg aan constructeurs is een belangrijk motief voor dit artikel.
De geherformuleerde afleiding is getoetst door die in te bouwen in het programma XFEM4U. Het daarin gebruikte elementtype wordt in het Engels aangeduid als hybrid element omdat zowel een veronderstelling wordt gemaakt voor het verloop van de zakkingen als voor de momenten. De methode is niet nieuw, ook niet voor Nederland, want de bouwdiensten van Rijkswaterstaat gebruikten zulke elementen al in de jaren 70 van de vorige eeuw. Maar het elementtype wordt weinig meer genoemd nu overal in standaardpakketten als AxisVM, RFEM, Robot en Scia Engineer doorgaans andere elementen gebruikt worden. Hybride elementen zijn mooie elementen met een voor constructeurs duidelijke verdeling van de momenten over het oppervlak van het element. Ook is er zekerheid over betrouwbare dwarskrachten, wel belangrijk voor een correcte berekening van dwarskrachtwapening. Het opnieuw gebruiken van dit element mag men een herwaardering in de Nederlandse bouwwereld noemen.
Vanaf hier volgt een wapeningsbetoog in vier stappen. Eerst wordt het wapenen voor schijfkrachten samengevat en daarna het wapenen op plaatmomenten in de situatie dat geen dwarskrachtwapening nodig is. In de derde stap vindt de uitbreiding plaats naar het wapenen van platen op zowel moment als dwarskracht. Het combineren van schijf- en plaatwapening zoals o.a. nodig is in schaalconstructies is dan een eenvoudige laatste vierde stap.
Een lineair-elastische EEM-berekening van schijven heeft als resultaat het verloop van de schijfkrachten nxx, nyy en nxy. Deze krachten zijn gedefinieerd per eenheid van plaatbreedte en aangrijpend in het middenvlak van de schijf (fig. 1). De krachten nxx en nyy zijn normaalkrachten en nxy is de schuifkracht, alle drie positief zoals getekend. De eveneens getekende schuifkracht nyx is gelijk aan nxy.
De spanningstoestand in een punt van de schijf ligt vast met de drie onafhankelijke schijfkrachten nxx, nyy en nxy, terwijl we doorgaans maar in twee richtingen willen wapenen. We gaan in dit rapport uit van orthogonale wapening evenwijdig aan de x-as en y-as. Doel is om de wapeningskrachten nsx en nsy te bepalen op basis waarvan de wapening wordt gekozen. Hierin staat de subscript s voor staal (steel in het Engels). Hoewel de basis van de beschouwing bestaat uit lineair-elastische EEM-resultaten gaat men er voor het vaststellen van de wapening van uit dat lokaal plastische overwegingen zijn toegestaan.
De wapeningskrachten voor de schijfkrachten nxx en nyy leveren geen moeilijkheden op. Die zijn nsx=nxx en nsy=nyy. Maar hoe op de schuifkracht nxy moet worden gewapend ligt niet voor de hand. De gebruikelijke oplossing is om de schuifkracht te vervangen door drie lijnspanningen, een trekspanning in horizontale richting, een trekspanning in verticale richting en een drukspanning in diagonale richting. De trekspanningen worden opgenomen door wapening en de drukspanning door beton. In dit rapport leiden we de lijnspanningen af met behulp van de vakwerkanalogie, met verwijzing naar figuur 2.
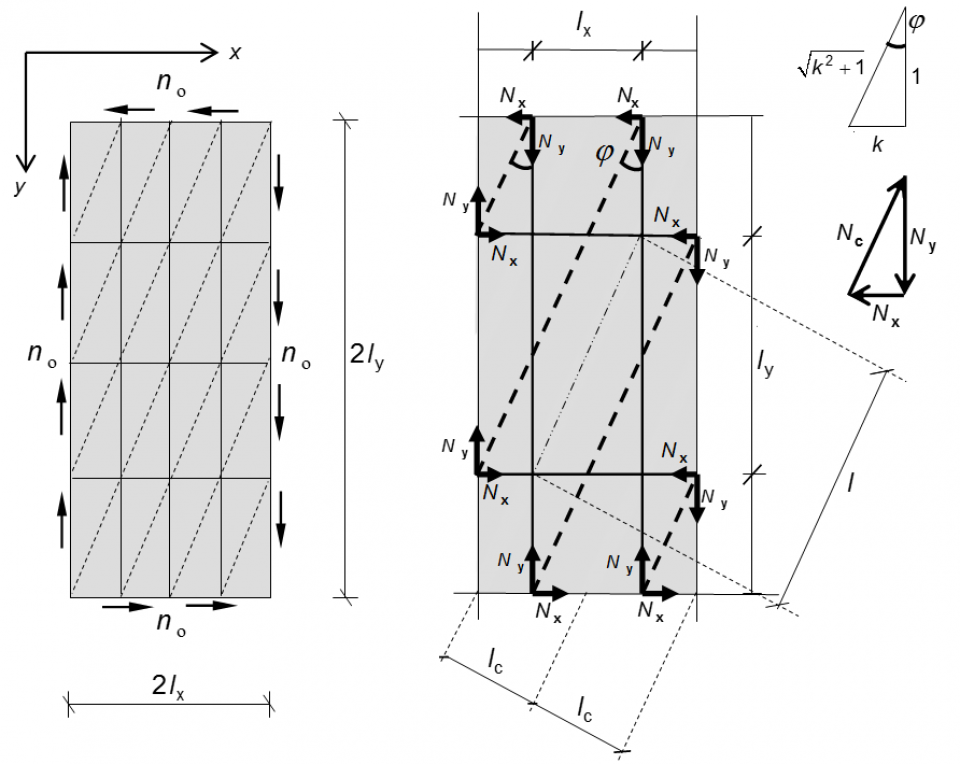
Figuur 2. Ontbinden van de schuifkracht no in drie lijnspanningstoestanden. Links positieve schuifkrachten no en de drie lijnspanningen, rechts het gebruikte vakwerk.
Om meer dan een reden is het handig om in de afleiding de schuifkracht nxy de kortere naam no te geven. Het linkerdeel van figuur 2 toont een schijfdeel met een homogene schuifkracht no per eenheid van lengte als belasting. De drie lijnspanningstoestanden zijn ingetekend. In de getrokken horizontale en verticale lijnen heerst trek en in de diagonale gestreepte lijnen druk. In het rechterdeel van figuur 2 is het vervangende vakwerkmodel getekend met twee horizontale en twee verticale trekstaven. De diagonalen maken een hoek φ met de verticaal. De onderlinge afstand van de horizontale trekstaven is ly en van de verticale lx. De vier trekstaven sluiten een rechthoek in met een diagonaallengte l. De hart-op-hart afstand van de diagonalen is lc waarin c staat voor het Engelse woord concrete (beton). De lengten lx , ly en lc laten zich op basis van de geometrie van figuur 2 op eenvoudige wijze in l en φ uitdrukken:
lx = l sin φ
ly = l cos φ (1)
lc = l sin φ cos φ
Het heeft zin om voor de tangens van de hoek φ een eigen symbool k in te voeren:
k = tan φ (2)
Met vergelijking (1) kan vergelijking (2) worden omgevormd tot:
.png) (3)
(3)
Voor de horizontale en verticale trekstaven geldt de tekenafspraak dat de kracht positief is. De trekkrachten zijn respectievelijk Nx, en Ny. In de diagonale staven treedt een drukkracht Nc op, waarin de subscript c staat voor het Engelse woord concrete (beton). Deze kracht is positief voor druk.
De krachten Nx en Ny kunnen worden uitgedrukt in de schuifkracht no en de lengten ly en lx. Langs de twee horizontale randen is de totale schuifkracht 2 no lx en deze wordt geconcentreerd in twee knopen met elk de kracht Nx. Evenzo gebeurt langs de twee verticale randen. Daaruit volgt:
Nx = no lx
Ny = no ly (4)
Door Nx te delen door ly en Ny door lx worden de wapeningskrachten nsxo en nsyo per eenheid van breedte gevonden ten gevolge van de schuifkracht no:
.png) (5)
(5)
De twee wapeningskrachten Nx en Ny en de betondrukkracht Nc maken in elke knoop evenwicht met elkaar. De grootte van Nc kan worden berekend met de formule van Pythagoras, op basis van het krachtenschema geheel rechts in figuur 2:
.png)
Met de vergelijkingen (1) en (4) leidt uitwerking tot:
.png)
De eenvoudige oplossing voor Nc wordt:
Nc = no l (7)
Deze drukkracht moet gespreid worden over de diagonaalbreedte lc wat leidt tot de drukkracht nc per eenheid van breedte:
.png) (8)
(8)
Uit de tekening rechtsboven in figuur 2 lezen we af:
1.png) (9)
(9)
waarmee vergelijking (8), na uitwerking, overgaat in:
.png) (10)
(10)
Samen met de wapeningskrachten voor nxx en nyy gaan de wapeningskrachten van vergelijking (5) over in (we schrijven weer nxy in plaats van no):
.png) (11)
(11)
Op de wapening in x-richting heeft de schuifkracht nxy invloed met het gewicht k en op de wapening in y-richting met het gewicht 1/k. Als niet de hoek φ tussen de diagonaal en de verticaal was gekozen, maar de hoek tussen de diagonaal en de horizontaal (hier θ genoemd) en gewerkt zou zijn met k = tan θ zou dat juist omgekeerd zijn. Omdat φ en θ samen π/2 zijn wisselen k en 1/k in vergelijking (11) dan van plaats. Op vergelijking (10) voor de diagonaalkracht heeft het geen invloed omdat daar de som van k en 1/k gebruikt wordt. De uitruil tussen φ en θ zal hierna gebruikt worden als het wapenen op dwarskracht wordt beschouwd.
Tot hier is geen keus gemaakt voor de hoek φ. Veronderstellend dat lokaal herverdeling mogelijk is kan de hoek φ vrij worden gekozen, anders gezegd kan voor k een keuze worden gemaakt. De wapening voor nxx en nyy kunnen we niet beïnvloeden, maar wel die voor nxy. Die wapening wordt minimaal als de som k +1/k minimaal is. Dat is het geval voor k = 1, zoals uit figuur 3 blijkt.
Reacties
arie koot - zonneveld 14 november 2023 17:24
In berekening wordt uitgegaan van orthogonale wapening. Maar als dit niet zo is? bijvoorbeeld twee richting wapening onder een hoek van 60 graden. Hoe gaat het dan?